Cách tìm Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác cực hay - Toán lớp 11

---

Cách tìm Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác cực hay

Với Cách tìm Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

Để tìm được giá trị lớn nhất;giá trị nhỏ nhất của hàm số ta cần chú ý:

+ Với mọi x ta luôn có: - 1 ≤ cosx ≤ 1; -1 ≤ sinx ≤ 1

+Với mọi x ta có: 0 ≤ |cosx| ≤ 1 ;0 ≤ |sinx| ≤ 1

+ Bất đẳng thức bunhia –copski: Cho hai bộ số (a₁; a₂) và (b₁;b₂) khi đó ta có:

(a₁.b₁+ a₂.b₂ )² ≤ ( a₁²+ a₂² ).( b₁²+ b₂² )

Dấu “=” xảy ra khi: a₁/a₂ = b₁/b₂

+ Giả sử hàm số y= f(x) có giá trị lớn nhất là M và giá trị nhỏ nhất là m. Khi đó; tập giá trị của hàm số là [m; M].

+ Phương trình : a. sinx+ b. cosx= c có nghiệm khi và chỉ khi a² + b² ≥ c²

B. Ví dụ minh họa

Ví dụ 1. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y= 1- 2|cos3x|.

A. M=3 ; m= - 1.

B. M= 1 ; m= -1.

C. M=2 ;m= -2.

D. M=0 ; m= -2.

Lời giải:.

Chọn B.

Với mọi x ta có : - 1 ≤ cos3x ≤ 1 nên 0 ≤ |cos3x| ≤ 1

⇒ 0 ≥ -2|cos3x| ≥ -2

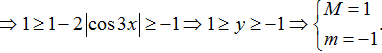
Ví dụ 2: Hàm số y= 1+ 2cos²x đạt giá trị nhỏ nhất tại x= x₀. Mệnh đề nào sau đây là đúng?

A.x₀=π+k2π, kϵZ .

B.x₀=π/2+kπ, kϵZ .

C.x₀=k2π, kϵZ .

D.x₀=kπ ,kϵZ .

Lời giải:.

Chọn B.

Ta có - 1 ≤ cosx ≤ 1 ⇒ - 0 ≤ cos²x ≤ 1 ⇒ 1 ≤ 1+2cos²x ≤ 3

Do đó giá trị nhỏ nhất của hàm số bằng 1 .

Dấu ‘=’ xảy ra khi cosx=0 ⇒ x=π/2+kπ, kϵZ .

Ví dụ 3: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y= sin2x+ 2cos2x.

A.M= 3 ;m= 0

B. M=2 ; m=0.

C. M=2 ; m= 1.

D.M= 3 ; m= 1.

Lời giải:.

Chọn C.

Ta có: y = sin² x+ 2cos²x = (sin²x+ cos²x) + cos²x = 1+ cos² x.

Do: -1 ≤ cosx ≤ 1 nên 0 ≤ cos² x ≤ 1 ⇒ 1 ≤ cos² x+1 ≤ 2

Suy ra giá trị lớn nhất của hàm số là M= 2 và giá trị nhỏ nhất của hàm số là m= 1

Ví dụ 4: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y= 4sinx - 3

A.M= 1; m= - 7

B. M= 7; m= - 1

C. M= 3; m= - 4

D. M=4; m= -3

Lời giải

Chọn A

Ta có : - 1 ≤ sinx ≤ 1 nên - 4 ≤ 4sinx ≤ 4

Suy ra : - 7 ≤ 4sinx-3 ≤ 1

Do đó : M= 1 và m= - 7

Ví dụ 5: Tìm tập giá trị T của hàm số y= -2cos2x + 10 .

A. [5; 9]

B.[6;10]

C. [ 8;12]

D. [10; 14]

Lời giải:

Chọn C

Với mọi x ta có : - 1 ≤ cos⁡2x ≤ 1 nên-2 ≤ -2cos2x ≤ 2

⇒ 8 ≤ -2cos2x+10 ≤ 12

Do đó tập giá trị của hàm số đã cho là : T= [ 8 ;12]

Ví dụ 6: Tính độ dài giá trị của hàm số y= 10- 2cos2x

A. 10

B. 8

C.6

D. 4

Lời giai

Với mọi x ta có: - 1 ≤ cos2x ≤ 1 nên-2 ≤ -2cos2x ≤ 2

Suy ra: 8 ≤ 10-2cos2x ≤ 12

Do đó; tập giá trị của hàm số đã cho là: [8; 12] và độ dài đoạn giá trị của hàm số là : 12 – 8= 4

Chọn D.

Ví dụ 7: Tính tổng giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số sau: y= √3 sin⁡( 2016x+2019)

A. - 4032

B. √3

C. -√3

D. 0

Lời giải:

Chọn D

Với mọi x ta có :- 1 ≤ sin⁡(2016x+2019) ≤ 1

⇒ -√3 ≤ √3sin⁡(2016x+2019) ≤ √3

Do đó giá trị nhỏ nhất của hàm số là -√3 và giá trị lớn nhất của hàm số là √3

⇒ Tổng giá trị lớn nhất và nhỏ nhất của hàm số là - √3+ √3=0

Ví dụ 8: Tìm giá trị nhỏ nhất m của hàm số y= 1/(1+sinx)

A. m= 1/2

B. m= 1/√2

C. m= 1

D. m= √2

Lời giải:

Chọn A

Điều kiện xác định : sinx ≠ -1 hay x ≠ (- π)/2+k2π

+ Với mọi x thỏa mãn điều kiện ta có : - 1<sinx ≤ 1 nên sinx + 1 > 0

+ Nếu mẫu 1+ sinx > 0 thì hàm số đạt giá trị nhỏ nhất khi và chỉ khi 1+ sinx đạt giá trị lớn nhất

Hay 1+ sinx=2 < ⇒ sinx= 1( thỏa mãn điều kiện) .

Khi đó ymin = 1/2

Vậy hàm số đạt giá trị nhỏ nhất là 1/2 khi sinx= 1

Ví dụ 9: Tìm giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số: y= 2018sin( 9x+π/100)+2000

A. m=18 ; M=4018

B. m = -18; M= 18

C. m=-18; M= 4018

D. Đáp án khác

Lời giải:

Chọn C

Hàm số xác định trên R.

Với mọi x ta có: - 1 ≤ sin( 9x+π/100) ≤ 1 nên - 2018 ≤ 2018sin( 9x+π/100) ≤ 2018

⇒ -18 ≤ 2018sin( 9x+π/100)+2000 ≤ 4018

⇒ giá trị nhỏ nhất của hàm số là -18 khi sin( 9x+π/100)=-1

Giá trị lớn nhất của hàm số là 4018 khi sin( 9x+π/100)=1

Ví dụ 10: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y= ∜sinx- √cosx.

A. m= -1; M=1.

B. m = 0; M=1

C. m= -1;M=0

D. m= -1 và M không tồn tại.

Lời giải:

Chọn A

Với mọi x thỏa mãn điều kiện : sinx > 0 và cosx > 0 .Ta có:

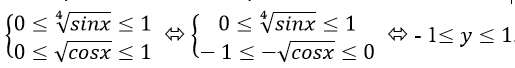
Vậy hàm số đạt giá trị nhỏ nhất là m= – 1 khi: (sinx=0 và cosx=1 ⇒ x= k2π.

Hàm số đạt giá trị lớn nhất là M=1 khi (sinx=1 và cosx=0 ⇒ x= π/2+k2π.

Ví dụ 11. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số : y= cos² x – 6cosx + 11. Tính M.m

A.30

B.36

C.27

D.24

Lời giải:

Ta có: cos² x – 6cosx +11 = ( cos²x – 6cosx + 9) +2 = (cosx -3)² + 2

Do - 1 ≤ cosx ≤ 1 ⇒ - 4 ≤ cosx-3 ≤ -2

⇒ 0 ≤ (cosx-3)^2 ≤ 16

⇒ 2 ≤ (cosx-3)^2+2 ≤ 18

Suy ra:M= 18 và m= 2 nên M. m= 36.

Chọn B.

Ví dụ 12. Gọi M và lần lượt là giá trị lớn nhất; giá trị nhỏ nhất của hàm số

y=(cosx+2sinx+3)/(2cosx-sinx+4). Tính S= M+11m

A.4

B.5

C. 6

D. 8

Lời giải:.

Gọi y₀ là một giá trị của hàm số.

Khi đó phương trình y₀=(cosx+2sinx+3)/(2cosx-sinx+4) có nghiệm.

⇒ y₀.( 2cosx- sinx + 4) = cosx +2sinx + 3 có nghiệm

⇒ 2y₀.cosx – sinx.y0 + 4y₀- cosx – 2sinx – 3=0 có nghiệm

⇒ ( 2y₀ -1)cosx – ( y₀+2).sinx =3- 4y₀ (*)

Phương trình (*) có nghiệm khi và chỉ khi :

(2y₀-1)² + ( y₀ + 2)² ≥ (3-4y₀)²

⇒ 4y₀² – 4y₀ +1 +y₀² +4y₀ + 4 ≥ 9-24y₀+16y₀²

⇒ 11y₀² – 24y₀ + 4 ≤ 0  2/11 ≤ y₀ ≤ 2

Suy ra: M=2 và m=2/11 nên S= M+ 11m= 4

Chọn A.

Ví dụ 13. Cho hàm số y= √(1+2sin² x)+ √(1+2〖cos² x)-1. Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số. Khi đó; giá trị M+ m gần với giá trị nào nhất?

A. 3,23

B. 3,56

C. 2,78

D.2,13

Lời giải:

+ Xét t= √(1+2sin² x)+ √(1+2cos² x)

⇒ t² = 1+ 2sin² x+ 1+ 2cos² x+ 2. √((1+2sin² x).( 1+2cos² x) )

=4+2√(3+ sin² 2x)

Mà sin²2x ≥ 0 nên t² ≥ 4+ 2√3

Mà t > 0 nên t ≥ √(4+2√3) =1+ √3

Suy ra: y= t-1 ≥ √3

Dấu “=” xảy ra khi sin2x=0 .

+ Lại có:

√(1+2sin² x)+ √(1+2cos² x) ≤ √((1^2+ 1^2 ).( 1+2sin²x+ 1+2cos² x) )= 2√2

⇒ y= √(1+2sin² x)+ √(1+2cos² x)-1 ≤ 2√2-1

Dấu “=” xảy ra khi sin2 x= cos2x

Vậy {(m= √3 và M=2√2-1) ⇒ M+ m≈3,56

Chọn B.

C. Bài tập vận dụng

Câu 1:Gọi M; m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=8sin²x+3cos2x . Tính P= M- 2m.

A. P= - 1

B. P= 1

C. P= 2

D. P=0

Lời giải:

Chọn A.

Ta có: y = 8sin2 x + 3cos2x = 8sin2x + 3( 1 – 2sin2x ) = 2sin2x+ 3.

Mà -1 ≤ sinx ≤ 1 ⇒ 0 ≤ sin^x ≤ 1 ⇒ 3 ≤ 2sin^x+3 ≤ 5 ⇒ 3 ≤ y ≤ 5.

Suy ra: M= 5 và m= 3

Do đó: P = 5- 2.3= - 1

Câu 2:Tìm giá trị lớn nhất M của hàm số y= 4sin2x + 3.cos2x .

A. M= 3

B. M= 1

C. M= 5

D. M= 4

Lời giải:

Chọn C.

Ta có: y = 4sin2x+ 3cos2x = 5.( 4/5.sin2x+ 3/5 cos2x).

Đặt cosα= 4/5 và sinα= 3/5

Khi đó: y= 5( cosα.sin2x+sinα.cos2x)=5.sin⁡( α+2x)

⇒ - 5 ≤ y ≤ 5

Suy ra M= 5.

Câu 3:Gọi M ; m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y= sin²x – 4sinx+ 5. Tính M+ m.

A.3

B.8

C.10

D.12

Lời giải:

Chọn D.

Ta có: y= sin²x – 4sinx+ 5= ( sinx- 2)² + 1.

Do: -1 ≤ sinx ≤ 1 nên-3 ≤ sinx-2 ≤ -1

⇒ 1 ≤ ( sinx-2)² ≤ 9 ⇒ 2 ≤ ( sinx-2)²+1 ≤ 10 .

Suy ra: M=10 và m = 2

Do đó; M+ m = 12

Câu 4:Cho hàm số y= cos²x- cosx có tập giá trị là T. Hỏi có tất cả bao nhiêu giá trị nguyên thuộc T.

A. 1

B. 2

C. 3

D. 4

Lời giải:

Chọn C.

Ta có: cos²x- cosx = (cosx- 1/2)²- 1/4 .

Do - 1 ≤ cosx ≤ 1 nên (- 3)/2 ≤ cosx- 1/2 ≤ 1/2

⇒ 0 ≤ ( cosx- 1/2)² ≤ 9/4 ⇒ (- 1)/4 ≤ ( cosx- 1/2)²- 1/4 ≤ 2.

Do đó (- 1)/4 ≤ y ≤ 2. Vậy tập giá trị của hàm số là [(- 1)/4;2]

⇒ Trong đoạn [ -1/4;2] có ba giá trị nguyên thỏa mãn là 0; 1 và 2.

Do đó có 3 giá trị thỏa mãn.

Câu 5:Hàm số y= cos²x+ 2sinx+ 2 đạt giá trị nhỏ nhất tại x0. Mệnh đề nào sau đây là đúng.

A. x= (-π)/2+k2π.

B. x= π/2+k2π.

C. x= k π

D. x= k2π

Lời giải:

Chọn B.

Ta có: cos²x+ 2sinx+ 2 = 1- sin²x+ 2sinx + 2= - sin²x + 2sinx+ 3 = - (sinx-1)² + 4

Mà - 1 ≤ sinx ≤ 1 nên-2 ≤ sinx-1 ≤ 0

Suy ra: 0 ≤ ( sinx-1)² ≤ 4 ⇒ -4 ≤ - (sinx-1)² ≤ 0

⇒ 0 ≤ 4 - (sinx-1)² ≤ 4

Suy ra giá trị nhỏ nhất của hàm số bằng 0.

Dấu “=” xảy ra khi và chỉ khi sinx= 1 ⇒ x= π/2+k2π.

Câu 6:Tìm giá trị lớn nhất M và nhỏ nhất m của hàm số y= sin⁴x -2 cos²x+ 1.

A.M= 2; m= - 2

B.M=1; m=0

C.M=4;m= - 1

D M=2;m= - 1

Lời giải:

Chọn D.

Ta có: sin⁴x- 2cos²x + 1= sin⁴x – 2( 1- sin²x) + 1

= sin⁴x + 2sin²x - 1 = ( sin² x +1)²2 - 2

Mà: 0 ≤ sin² x ≤ 1 nên 1 ≤ sin² x+1 ≤ 2

Suy ra: 1 ≤ ( sin² x+1)² ≤ 4 ⇒ -1 ≤ ( sin² x+1)²-2 ≤ 2 .

Nên M= 2; m= - 1

Câu 7:Tìm giá trị nhỏ nhất của hàm số y= 4sin⁴x – cos4x.

A. - 3

B. - 1

C. 3

D. 5

Lời giải:

Chọn B.

Ta có: y= 4sin⁴x – cos4x= 4.((1-cos2x)/2)²-(2cos² 2x-1)

= 1- 2cos2x+ cos²2x – 2cos²x + 1

= - cos⁴2x - 2cos2x + 2 = - (cos2x+ 1)² + 3

Mà -1 ≤ cos2x ≤ 1 ⇒ 0 ≤ cos2x+1 ≤ 2 ⇒ 0 ≤ (cos2x+1)² ≤ 4 ⇒ -1 ≤ -(cos2x+1)²+3 ≤ 3

Suy ra m= - 1.

Câu 8:Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y= 2( sinx - cosx). Tính P= M+ 2m.

A. 2

B. - 2√2

C. - √2

D. 4√2

Lời giải:

Chọn B

Ta có : 2( sinx- cosx)=2√2 sin⁡( x- π/4)

Với mọi x thì : - 1 ≤ sin⁡( x- π/4) ≤ 1

⇒ - 2√2 ≤ 2√2.sin⁡( x- π/4) ≤ 2√2

Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho là M= 2√2 và m= -2√2

⇒ P= M+ 2m= - 2√2

Câu 9:Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y= √(1- cos² x)+1là:

A. 2 và 1

B. 0 và 3

C. 1 và 3

D.1 và 1+ √2

Lời giải:

Ta có : √(1- cos² x)= √(sin² x)= |sinx|

Do đó; hàm số y= √(1- cos² x)+1=|sinx|+1

Với mọi x ta có: - 1 ≤ sinx ≤ 1 nên 0 ≤ |sinx| ≤ 1

⇒ 1 ≤ |sinx|+1 ≤ 2

⇒ giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho là 2 và 1.

Chọn A

Câu 10:Giá trị nhỏ nhất của hàm số y= 4sin² x+ 6cos²x+ 2 là

A. 4

B. 6

C. 8

D. 10

Lời giải:

Ta có: 4sin²x + 6cos² x+ 1= 2( 1- cos2x) + 3( 1+cos2x) + 2 = cos2x+ 7

Với mọi x ta luôn có: - 1 ≤ cos2x ≤ 1 nên 6 ≤ cos2x+7 ≤ 8

Suy ra: giá trị nhỏ nhất của hàm số là 6

Chọn B.

Câu 11:Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau

A.max y=4,min y=3/4

B.max y=3,min y=2

C.max y=4,min y=2

D.max y=3,min y=3/4

Lời giải:

Đặt t=sin²x, 0 ≤ t ≤ 1 ⇒ cos2x=1-2t

⇒ y= 2t+(1-2t)²=4²-2t+1=(2t-1/2)²+3/4

Do 0 ≤ t ≤ 1 ⇒ -1/2 ≤ 2t-1/2 ≤ 3/2 ⇒ 0 ≤ (2t-1/2)² ≤ 9/4 ⇒ 3/4 ≤ y ≤ 3 .

Vậy max y=3 đạt được khi x=π/2+kπ .

min y=3/4 đạt được khi sin²x=1/4 .

Chọn D.

Câu 12:Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3sinx + 4cosx + 1

A. max y=6,min y=-2

B. max y=4,min y=-44

C. max y=6,min y=-4

D.max y=6,min y=-1

Lời giải:

Áp dụng bất đẳng thức bunhia- xcopski: (ac+bd)² ≤ (c²+d²)(a²+b²) .

Đẳng thức xảy ra khi a/c=b/d .

Ta có: (3sinx+4cosx)² ≤ (3²+4²)(sin²+cos²)=25

⇒ 5 ≤ 3sinx+4cosx ≤ 5 ⇒ -4 ≤ y ≤ 6

Vậy max y=6 , đạt được khi tanx=3/4 .

min y=-4 , đạt được khi tanx=-3/4.

Chọn C.

Câu 13:Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y=2sin²x+3sin2x-4cos²x

A. min y= -3√2 -1, max y=3√2 +1

B. min y= -3√2 -1, max y=3√2 -1

C. min y= -3√2 , max y=3√2 -1

D. min y= -3√2 -2, max y=3√2 -1

Lời giải:

Ta có: y= 2sin² x + 3sin2x - 4cos²x

= 1 – cos2x + 3sin2x - 2( 1+ cos2x)

=3sin2x-3cos2x-1=3√2sin(2x-π/4)-1

Mà -1 ≤ sin(2x- π/4) ≤ 1 ⇒ - 3√2 ≤ 3√2sin⁡(2x- π/4) ≤ 3√2

⇒ - 3√2-1 ≤ 3√2sin⁡( 2x- π/4)-1 ≤ 3√2-1

Suy ra min y= -3√2 -1, max y=3√2 -1 .

Chọn B.

Câu 14:Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=sin²x+3sin2x+3cos²x

A. min y= 2+√10 , max y=2-√10

B. min y= 2+√5, max y=2+√5

C. min y= 2+√2, max y=2-√2

D. min y= 2+√7, max y=2-√7

Lời giải:

Ta có: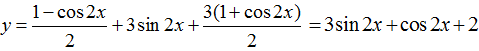

Áp dụng bất đẳng thức bunhia- xcopki ta có :

- √(3²+ 1² ) ≤ 3sin2x+cos2x ≤ √(3²+ 1² )

Suy ra : -√10 ≤ 3sin2x+cos2x ≤ √10

⇒ 2-√10 ≤ y ≤ 2+√10

Từ đó ta có được: maxy=2+√10;miny=2-√10.

Chọn A.

Câu 15:Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y=sinx+ √(2-sin²)

A.min y= 0, max y=3

B.min y= 0, max y=4

C.min y= 0, max y=6

D.min y= 0, max y=2

Lời giải:

Ta có 0 ≤ y ∀x và y²=2+2sin√(2-sin²)

Mà 2|sin√(2-sin²)| ≤ sin²+2-sin²=2

Suy ra 0 ≤ y² ≤ 4 ⇒ 0 ≤ y ≤ 4

min y=0 đạt được khi x=-π/2+k2π

max y=2 đạt được khi x=π/2+k2π

Chọn D.

Câu 16:Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y=(sin2x+2cos2x+3)/(2sin2x-cos2x+4)

A. min y= -2/11, max y=2

B. min y= 2/11, max y=3

C. min y= 2/11, max y=4

D. min y= 2/11, max y=2

Lời giải:

+ Áp dụng bất đẳng thức bunhia-xcopski ta có:

(2sin2x – cos2x)² ≤ (2²+(-1)²). ( sin²2x + cos²2x) = 5

⇒ -√5 ≤ 2sin2x-cos2x ≤ √5

⇒ 4-√5 ≤ 4+ 2sin2x-cos2x ≤ 4+√5

⇒ 4+ 2sin2x- cos2x > 0 với mọi x.

+ Ta có:

y=(sin2x+2cos2x+3)/(2sin2x-cos2x+4)

⇒ y. 2sin2x – y.cos2x + 4y = sin2x +2cos2x + 3

⇔ (2y-1)sin2x-(y+2)cos2x=3-4y (*)

Phương trình (*) có nghiệm khi và chỉ khi:

⇒ (2y-1)²+(y+2)² ≥ (3-4y)²

⇔ 11y²-24y+4 ≤ 0 ⇔ 2/11 ≤ y ≤ 2

Suy ra: min y= 2/11, max y=2 .

Chọn D.

Câu 17:Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=(2sin²3x+4sin3xcos3x+1)/(sin6x+4cos6x+10)

A. min y= (11-9√7)/83, max y=(11+9√7)/83

B. min y= (22-9√7)/11, max y=(22+9√7)/11

C. min y= (33-9√7)/83, max y=(33+9√7)/83

D. min y= (22-9√7)/83, max y=(22+9√7)/83

Lời giải:

+Áp dụng bất đẳng thức bunhia- xcopski ta có:

( sin6x+4cos6x)² ≤ (1²+4²). ( sin²6x+ cos²6x)= 17

⇒ -√17 ≤ sin6x+4cos6x ≤ √17

⇒ sin6x+4cos6x+10 ≥ 10-√17 > 0 ∀x thuộc R

Do đó; hàm số xác định với mọi x.

+ ta có: y=(2sin6x-cos6x+2)/(sin6x+4cos6x+10)

⇒ (y-2)sin6x+(4y+1)cos6x=2-10y

Phương trình trên có nghiệm khi và chỉ khi:

⇒ (y-2)²+(4y+1)² ≥ (2-10y)² ⇔ 83y²-44y-1 ≤ 0

⇒ (22-9√7)/83 ≤ y ≤ (22+9√7)/83.

Suy ra: min y= (22-9√7)/83, max y=(22+9√7)/83

Chọn D.