Lý thuyết Đại cương về đường thẳng và mặt phẳng hay, chi tiết nhất - Toán lớp 11
Lý thuyết Đại cương về đường thẳng và mặt phẳng hay, chi tiết nhất
Tài liệu Lý thuyết Đại cương về đường thẳng và mặt phẳng hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về đường thẳng và mặt phẳng từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

1. Mở đầu về hình học không gian
Hình học không gian có các đối tượng cơ bản là điểm, đường thẳng và mặt phẳng.
Quan hệ thuộc: Trong không gian:
a. Với một điểm A và một đường thẳng d có thể xảy ra hai trường hợp:
Điểm A thuộc đường thẳng d, kí hiệu A ∈ d.
Điểm A không thuộc đường thẳng, kí hiệu A ∉ d.
b. Với một điểm A và một mặt phẳng (P) có thể xảy ra hai trường hợp:
Điểm A thuộc mặt thẳng (P), kí hiệu A ∈ (P).
Điểm A không thuộc đường thẳng, kí hiệu A ∉ (P).
2. Các tính chất thừa nhận của hình học không gian
Tính chất thừa nhận 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
Tính chất thừa nhận 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
Tính chất thừa nhận 3: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.
Tính chất thừa nhận 4: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
Tính chất thừa nhận 5: Trong mỗi mặt phẳng, các kết đã biết của hình học phẳng đều đúng.
Định lí: Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

3. Điều kiện xác định mặt phẳng
Có bốn cách xác định trong một mặt phẳng:
Cách 1: Một mặt phẳng được xác định nếu biết nó đi qua ba điểm A, B, C không thẳng hàng của mặt phẳng, kí hiệu (ABC).
Cách 2: Một mặt phẳng được xác định nếu biết nó đi qua một đường thẳng d và một điểm A không thuộc d, kí hiệu (A, d).
Cách 3: Một mặt phẳng được xác định nếu biết nó đi qua hai đường thẳng a, b cắt nhau, kí hiệu (a, b).
Cách 4: Một mặt phẳng được xác định nếu biết nó đi qua hai đường thẳng a, b song song, kí hiệu (a, b).
4. Hình chóp và tứ diện
Định nghĩa: Cho đa giác A1A2…An và cho điểm S nằm ngoài mặt phẳng chứa đa giác đó. Nối S với các đỉnh A1, A2,…, An ta được n miền đa giác SA1A2, SA2A3,…, SAn-1An.
Hình gồm n tam giác đó và đa giác A1A2A3...An được gọi là hình chóp S.A1A2A3…An.
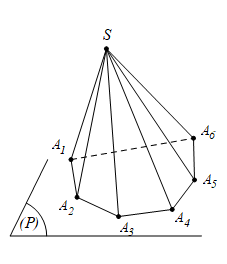
Trong đó:
Điểm S gọi là đỉnh của hình chóp.
Đa giác A1A2…An gọi là mặt đáy của hình chóp.
Các đoạn thẳng A1A2, A2A3, …, An-1An gọi là các cạnh đáy của hình chóp.
Các đoạn thẳng SA1, SA2,…, SAn gọi là các cạnh bên của hình chóp.
Các miền tam giác SA1A2, SA2A3,…,SAn-1An gọi là các mặt bên của hình chóp.
Nếu đáy của hình chóp là một miền tam giác, tứ giác, ngũ giác,… thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,…

Chú ý
a.Hình chóp tam giác còn được gọi là hình tứ diện.
b. Hình tứ diện có bốn mặt là những tam giác đều hay có tất cả các cạnh bằng nhau được gọi là hình tứ diện đều.

