Lý thuyết Đường thẳng và mặt phẳng song song hay, chi tiết nhất - Toán lớp 11
Lý thuyết Đường thẳng và mặt phẳng song song hay, chi tiết nhất
Tài liệu Lý thuyết Đường thẳng và mặt phẳng song song hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Đường thẳng và mặt phẳng song song từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

1. Vị trí tương đối của đường thẳng và mặt phẳng
Cho đường thẳng a và mặt phẳng (P). Căn cứ vào số điểm chung của đường thẳng và mặt phẳng ta có ba trường hợp sau:
a. Đường thẳng a và mặt phẳng (P) không có điểm chung, tức là:
a ⋂ (P) = ∅ ⇔ a // (P).
b. Đường thẳng a và mặt phẳng (P) chỉ có một điểm chung, tức là:
a ⋂ (P) = A ⇔ a cắt (P) tại A.
c. Đường thẳng a và mặt phẳng (P) có hai điểm chung, tức là:
a ⋂ (P) = {A, B} ⇔ a ∈ (P).
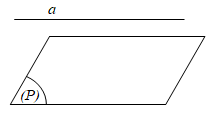
a ⋂ (P) = ∅ ⇔ a // (P).
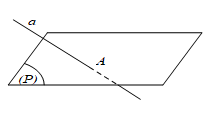
a ⋂ (P) = A ⇔ a cắt (P)
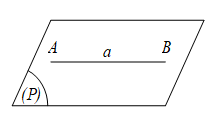
a ⋂ (P) = {A, B} ⇔ a ∈ (P).

2. Điều kiện để một đường thẳng song song với một mặt phẳng
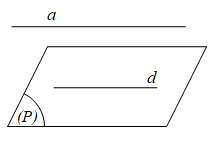
Định lí 1: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nào đó trong (P) thì a song song với (P).
Tức là, a ∉ (P) thì nếu:
a // d ∈ (P) ⇒ a // (P).
3. Tính chất
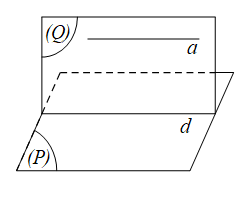
Định lí 2: Nếu đường thẳng a song song với mặt phẳng (P) thì mọi mặt phẳng (Q) chứa a mà cắt (P) thì sẽ cắt theo một giao tuyến song song với a.
Tức là, nếu 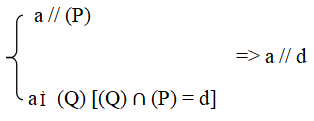
Hệ quả 1: Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó trong mặt phẳng.
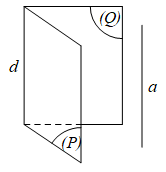
Hệ quả 2: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến (nếu có) của chúng song song với đường thẳng đó.
Tức là: 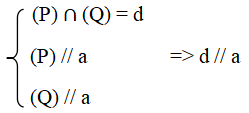
Hệ quả 3: Nếu a và b là hai đường thẳng chéo nhau thì qua a có một và chỉ một mặt phẳng song song với b.

