Lý thuyết Hai đường thẳng vuông góc hay, chi tiết nhất - Toán lớp 11

Lý thuyết Hai đường thẳng vuông góc hay, chi tiết nhất

Tài liệu Lý thuyết Hai đường thẳng vuông góc hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Hai đường thẳng vuông góc từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

I. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ TRONG KHÔNG GIAN

1. Góc giữa hai vectơ trong không gian

Định nghĩa

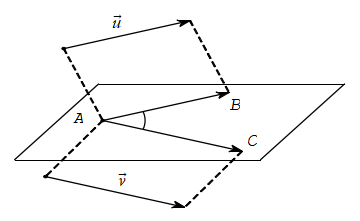
    Trong không gian, cho u→ và v→ là hai vectơ khác 0→. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho AB→ = u→, AC→ = v→. Khi đó ta gọi góc BAC ( 0° ≤ ∠BAC ≤ 180°) là góc giữa hai vectơ u→ và v→ trong không gian, kí hiệu là (u→, v→).

2. Tích vô hướng của hai vectơ trong không gian

Định nghĩa

    Trong không gian, cho hai vectơ u→ và v→ đều khác 0→. Tích vô hướng của hai vectơ u→ và v→ là một số, kí hiệu là u→.v→, được xác định bởi công thức:

            u→.v→ = |u→|.|v→|.cos(u→, v→)

Trong trường hợp u→ = 0→ hoặc v→ = 0→, ta quy ước u→.v→ = 0.

II. VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG

1. Định nghĩa

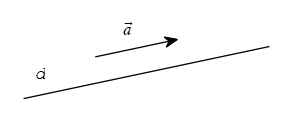
    Vectơ a→ khác 0→ được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ a→ song song hoặc trùng với đường thẳng d.

2. Nhận xét

    a) Nếu a→ là vectơ chỉ phương của đường thẳng d thì vectơ ka→ với k ≠ 0 cũng là vectơ chỉ phương của d.

    b) Một đường thẳng trong không gian hoàn toàn xác định nếu biết một điểm A thuộc d và một vectơ chỉ phương a→ của nó.

    c) Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai vectơ chỉ phương cùng phương.

III. GÓC GIỮA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN

1. Định nghĩa

    Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b.

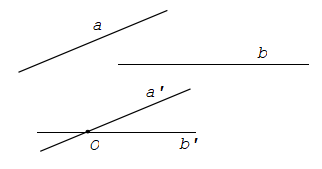
2. Nhận xét

    a) Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.

    b) Nếu u→ là vectơ chỉ phương của đường thẳng a và v→ là vectơ chỉ phương của đường thẳng b và (u→, v→) = α thì góc giữa hai đường thẳng a và b bằng α nếu 0° ≤ α ≤ 90° và bằng 180° – α nếu 90° < α < 180°. Nếu a và b song song hoặc trùng nhau thì góc giữa chúng bằng 0°.

IV. HAI ĐƯỜNG THẲNG VUÔNG GÓC

1. Định nghĩa

    Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90°.

Người ta kí hiệu hai đường thẳng a và b vuông góc với nhau là a ⊥ b.

2. Nhận xét

    a) Nếu u→ và v→ lần lượt là các vectơ chỉ phương của hai đường thẳng a và b thì: a ⊥ b ⇔ u→.v→ = 0.

    b) Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

    c) Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.