Lý thuyết Khoảng cách hay, chi tiết nhất - Toán lớp 11

Lý thuyết Khoảng cách hay, chi tiết nhất

Tài liệu Lý thuyết Khoảng cách hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Khoảng cách từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

I. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG, ĐẾN MỘT MẶT PHẲNG

1. Khoảng cách từ một điểm đến một đường thẳng

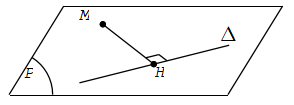
    Khoảng cách từ điểm M đến đường thẳng Δ là khoảng cách giữa hai điểm M và H trong đó H là hình chiếu của điểm M trên đường thẳng Δ.

2. Khoảng cách từ một điểm đến một mặt phẳng

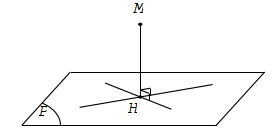
    Khoảng cách từ điểm M đến mặt phẳng (P) là khoảng cách giữa hai điểm M và H trong đó H là hình chiếu của điểm M trên mặt phẳng (P).

II. KHOẢNG CÁCH GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG, GIỮA HAI MẶT PHẲNG SONG SONG.

1. Khoảng cách giữa đường thẳng và mặt phẳng song song

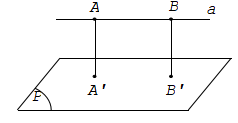
    Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm nào đó của a đến mặt phẳng (P).

2. Khoảng cách giữa hai mặt phẳng song song

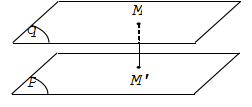
    Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.

III. KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU

1. Giả sử a và b là hai đường thẳng chéo nhau và a ⊥ b

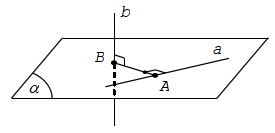
- Ta dựng mặt phẳng (α) chứa a và vuông góc với b tại B.

- Trong (α) dựng BA ⊥ (α) tại A, ta được độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.

2. Giả sử a và b là hai đường thẳng chéo nhau nhưng không vuông góc với nhau

Cách 1

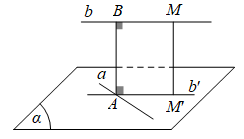
    + Ta dựng mặt phẳng (α) chứa a và song song với b.

    + Lấy một điểm M tùy ý trên b, dựng MM’ ⊥ (α) tại M’.

    + Từ M’ dựng b’ // b cắt a tại A.

    + Từ A dựng AB // MM’ cắt b tại B, độ dài đoạn thẳng AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.

Cách 2

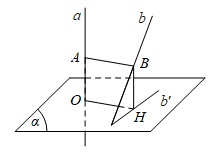
    + Ta dựng mặt phẳng (α) ⊥ a tại O, (α) cắt b tại I.

    + Dựng hình chiếu vuông góc của b là b’ trên mặt phẳng (α).

    + Trong mặt phẳng (α), vẽ OH ⊥ b’, H ∈ b’.

    + Từ H dựng đường thẳng song song với a và cắt b tại B.

    + Từ B dựng đường thẳng song song với OH cắt a tại A.

    + Độ dài đoạn thẳng AB là khoảng cách giữa hai đường thẳng chéo nhau a và b.