Lý thuyết Một số phương trình lượng giác thường gặp hay, chi tiết nhất - Toán lớp 11

Lý thuyết Một số phương trình lượng giác thường gặp hay, chi tiết nhất

Tài liệu Lý thuyết Một số phương trình lượng giác thường gặp hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Một số phương trình lượng giác thường gặp từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

I. TÓM TẮT LÝ THUYẾT

1. Phương trình bậc nhất với một hàm số lượng giác:

- Định nghĩa: Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng: at + b = 0, trong đó a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

- Ví dụ: 2sin x + 1 = 0 là phương trình bậc nhất đối với sin x,…

2. Phương trình bậc hai đối với một hàm số lượng giác

- Định nghĩa: Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng: at² + bt + c = 0, trong đó a, b, c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

- Ví dụ: 3tan² x 2tan x 1 = 0 là phương trình bậc hai đối với tan x

3. Phương trình bậc nhất đối với sin x và cos x

- Công thức biến đổi biểu thức asin x + bcos x :

    asin x + bcos x = 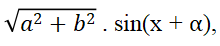        (1)

    với 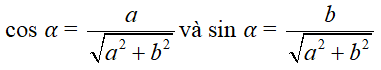(a² + b² ≠ 0)

- Xét phương trình: asin x + bcos x = c        (2)

với a, b, c ∈ R; a, b không đồng thời bằng 0 (a² + b² ≠ 0).

+ Nếu a = 0, b ≠ 0 hoặc a ≠ 0, b = 0, phương trình (2) có thể đưa ngay về phương trình lượng giác cơ bản.

+ Nếu a ≠ 0, b ≠ 0, ta áp dụng công thức (1)

II. PHƯƠNG PHÁP GIẢI

1. Phương trình bậc nhất với một hàm số lượng giác:

- Cách giải:

+ Bước 1: Chuyển vế

+ Bước 2: Chia hai vế của phương trình đã cho cho a

+ Bước 3: Giải phương trình lượng cơ bản.

- Ví dụ: Giải phương trình: 2sin x – √3 = 0

Ta có: 2sin x – √3 = 0 ⇔ 2sin x = √3

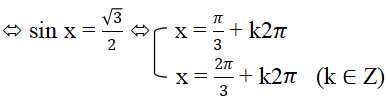
2. Phương trình bậc hai đối với một hàm số lượng giác:

- Cách giải:

+ Bước 1: Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có)

+ Bước 2: Giải phương trình bậc hai theo ẩn phụ này

+ Bước 3: Ta đưa về việc giải các phương trình lượng giác cơ bản.

- Ví dụ: Giải phương trình:

    3cos²x – 2cos x – 1 = 0

Đặt cos x = t với điều kiện –1 ≤ t ≤ 1 (*)

Khi đó phương trình đã cho có dạng: 3t² – 2t – 1 = 0 (**)

Giải phương trình (**) ta được hai nghiệm t₁ = 1 và t₂ = -1/3 thoả mãn điều kiện (*)

Vậy ta có:

TH1: cos x = 1 ⇔ x = k2π    (k ∈ Z).

TH2: cos x = -1/3 ⇔ x = ±arccos (-1/3) + k2π    (k ∈ Z)