Lý thuyết Tổng hợp chương Hàm số lượng giác - phương trình lượng giác hay, chi tiết nhất - Toán lớp 11

Lý thuyết Tổng hợp chương Hàm số lượng giác - phương trình lượng giác hay, chi tiết nhất

Tài liệu Lý thuyết Tổng hợp chương Hàm số lượng giác - phương trình lượng giác hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Tổng hợp chương Hàm số lượng giác - phương trình lượng giác từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

I. Các hàm số lượng giác:

1. Hàm số y = sin x

- Xác định với mọi x ∈ Z và –1 ≤ sin x ≤ 1;

- Là hàm số lẻ;

- Là hàm số tuần hoàn với chu kì 2π.

2. Hàm số y = cos x

- Xác định với mọi x ∈ Z và –1 ≤ cos x ≤ 1;

- Là hàm số chẵn;

- Là hàm số tuần hoàn với chu kì 2π.

3. Hàm số y = tan x

- Tập xác định là: D = R\{π/2 + kπ, k ∈ Z}.

- Là hàm số lẻ;

- Là hàm số tuần hoàn với chu kì π.

4. Hàm số y = cot x

- Tập xác định là: D = R\{kπ, k ∈ Z};

- Là hàm số lẻ;

- Là hàm số tuần hoàn với chu kì π.

II. Các phương trình lượng giác cơ bản:

1. Phương trình sin x = a

- Trường hợp |a| > 1: Phương trình (1) vô nghiệm

- Trường hợp |a| ≤ 1: Phương trình (1) có các nghiệm là

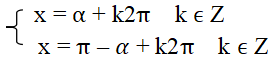
2. Phương trình cos x = a

- Trường hợp |a| > 1: Phương trình (2) vô nghiệm

- Trường hợp |a| ≤ 1: Phương trình (2) có các nghiệm là: x = ± α + k2π, k ∈ Z.

3. Phương trình tan x = a

- Điều kiện của phương trình là x ≠ π/2 + kπ, k ∈ Z.

- Nghiệm của phương trình tan x = a là: x = arctan a + kπ, k ∈ Z.

4. Phương trình cot x = a

- Điều kiện của phương trình là x ≠ kπ, k ∈ Z.

- Nghiệm của phương trình cot x = a là: x = arccot a + kπ, k ∈ Z.

III. Phương trình bậc nhất đối sin x và cos x

Xét phương trình: asin x + bcos x = c với a, b, c ∈ R; a, b không đồng thời bằng 0 (a² + b² ≠ 0).

- Nếu a = 0, b ≠ 0 hoặc a ≠ 0, b = 0, phương trình (2) có thể đưa ngay về phương trình lượng giác cơ bản.

- Nếu a ≠ 0, b ≠ 0, ta áp dụng công thức: asin x + bcos x =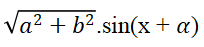

với (a² + b² ≠ 0)