Lý thuyết Phương trình lượng giác cơ bản hay, chi tiết nhất - Toán lớp 11

Lý thuyết Phương trình lượng giác cơ bản hay, chi tiết nhất

Tài liệu Lý thuyết Phương trình lượng giác cơ bản hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Phương trình lượng giác cơ bản từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

I. TÓM TẮT LÝ THUYẾT

1. Phương trình sin x = a (1)

- Trường hợp |a| > 1: Phương trình (1) vô nghiệm

- Trường hợp |a| ≤ 1: Phương trình (1) có các nghiệm là

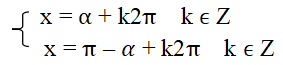
+ Nếu số thực α thoả mãn điều kiện

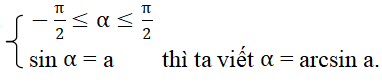
- Lưu ý:

+ Phương trình sin x = sin α, với α là một số cho trước, có các nghiệm là:

    x = α + k2π    k ∈ Z và x = π – α + k2π    k ∈ Z

Tổng quát: sin f(x) = sin g(x)

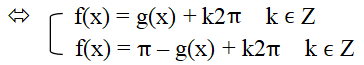
+ sin x = sin β°

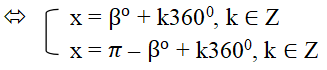
+ Các trường hợp đặc biệt:

    a = 1: Phương trình sin x = 1 có các nghiệm là: x = π/2 + k2π    k ∈ Z.

    a = –1: Phương trình sin x = –1 có các nghiệm là: x = -π/2 + k2π    k ∈ Z.

    a = 0: Phương trình sin x = 0 có các nghiệm là: x = x = kπ    k ∈ Z.

2. Phương trình cos x = a (2)

- Trường hợp |a| > 1: Phương trình (2) vô nghiệm

- Trường hợp |a| ≤ 1: Phương trình (2) có các nghiệm là

    x = ±α + k2π, k ∈ Z.

+ Nếu số thực α thoả mãn điều kiện:

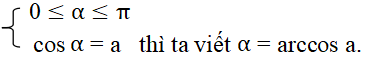
- Lưu ý:

+ Phương trình cos x = cosα, với α là một số cho trước, có các nghiệm là:

    x = ±α + k2π, k ∈ Z.

Tổng quát: cos f(x) = cos g(x) ⇔ f(x) = x = ±g(x) + k2π, k ∈ Z.

+ cos x = cos β° ⇔ x = ±β° + 360°, k ∈ Z.

+ Các trường hợp đặc biệt:

    a = 1: Phương trình cos x = 1 có các nghiệm là: x = k2π, k ∈ Z

    a = –1: Phương trình cos x = –1 có các nghiệm là: x = π + k2π, k ∈ Z

    a = 0: Phương trình cos x = 0 có các nghiệm là: x = π/2 + kπ, k ∈ Z.

3. Phương trình tan x = a (3)

- Điều kiện của phương trình là x ≠ π/2 + kπ, k ∈ Z.

- Nghiệm của phương trình tan x = a là:

    x = arctan α + kπ, k ∈ Z.

- Lưu ý:

+ Phương trình tan x = tan α, với α là một số cho trước, có các nghiệm là:

    x = α + kπ, k ∈ Z.

Tổng quát: tan f(x) = tan g(x) ⇒ f(x) = g(x) + kπ, k ∈ Z.

+ tan x = tan β° ⇔ x = β° + k180°, k ∈ Z.

4. Phương trình cot x = a (4)

- Điều kiện của phương trình là x ≠ kπ, k ∈ Z.

- Nghiệm của phương trình cot x = a là:

    x = arccot α + kπ, k ∈ Z.

- Lưu ý:

+ Phương trình cot x = cot α, với α là một số cho trước, có các nghiệm là:

    x = α + kπ, k ∈ Z.

Tổng quát: cot f(x) = cot g(x) ⇒ f(x) = g(x) + kπ, k ∈ Z.

+ Phương trình cot x = cot β° có các nghiệm là x = β° + k180° , k ∈ Z.