Cách giải Phương trình lượng giác không mẫu mực cực hay - Toán lớp 11

---

Cách giải Phương trình lượng giác không mẫu mực cực hay

Với Cách giải Phương trình lượng giác không mẫu mực cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Cách giải Phương trình lượng giác không mẫu mực cực hay từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

Để giải các phương trình lượng giác không mẫu mực ta cần sử dụng:

• Các công thức lượng giác: Công thức cộng; công thức nhân đôi; công thức biến đổi tổng thành tích; tích thành tổng ...

• Sử dụng các hằng đẳng thức đáng nhớ..

• Đánh giá: a2 ≥ 0 ; vế trái ≤ a; vế phải ≥ a. Từ đó; suy ra: Vế trái = vế phải= a.

• Đánh giá : Vế trái > a; vế phải < 0 nên phương trình vô nghiệm.....

B. Ví dụ minh họa

Ví dụ 1. Giải phương trình: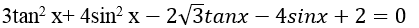

A.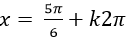

B.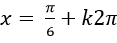

C.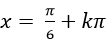

D. Cả A và C đúng

Lời giải

Chọn B.

Ví dụ 2. Giải phương trình: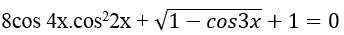

A.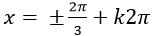

B.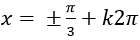

C.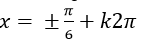

D. Đáp án khác

Lời giải

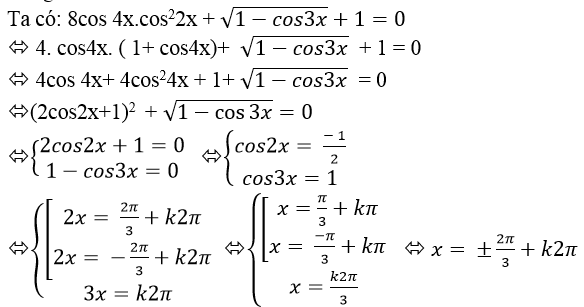
Chọn A.

Ví dụ 3. Giải phương trình: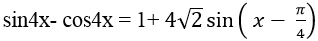

A.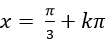

B.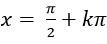

C. x= kπ

D.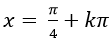

Lời giải

Ta có: sin4x- cos4x = 1+ 4√2 sin⁡( x- π/4)

⇒ sin 4x – ( 1+ cos4x) = 4(sinx – cosx)

⇒ 2.sin2x. cos2 x- 2cos²2x = 4( sinx- cosx)

⇒ 2cos 2x.( sin2x – cos 2x) – 4(sinx- cosx)= 0

⇒ 2(cos² x- sin² x). ( sin2x- cos2x) – 4.(sinx- cosx) = 0

⇒ 2. ( cosx- sinx) . ( cosx+ sinx). (sin2x- cos2x) + 4( cosx + sinx) = 0

⇒ 2. ( cosx – sinx) .[ (cosx+ sinx) ( sin2x- cos2x) + 2] = 0

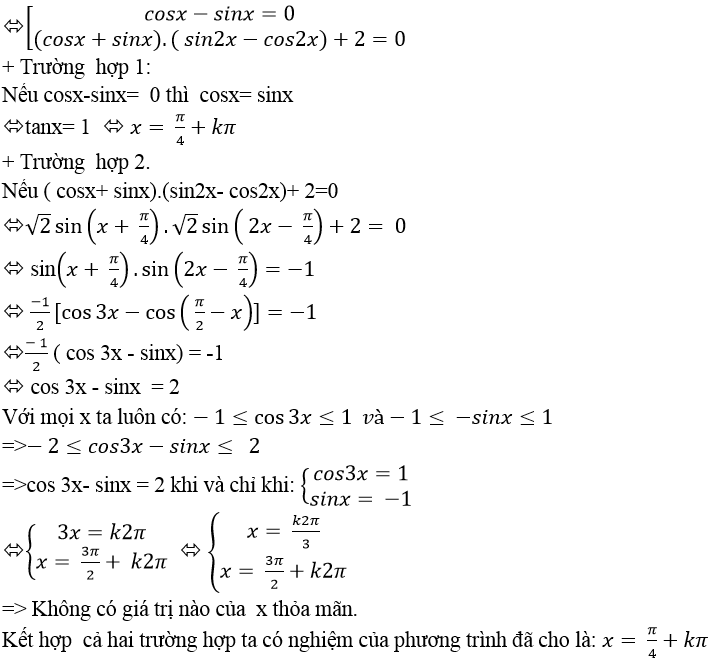
Chọn D.

Ví dụ 4. Giải phương trình sin3x. ( cosx- 2sin3x) + cos 3x.(1+ sinx- 2cos 3x) = 0

A. π/8+ kπ/2

B. k2π/3

C. kπ/4

D. Vô nghiệm

Lời giải

Ta có:

sin3x. ( cosx- 2sin3x) + cos 3x.(1+ sinx- 2cos 3x) = 0

⇒ sin3x. cosx – 2sin²3x + cos 3x + cos3x.sinx – 2cos²3x = 0

⇒ ( sin3x. cosx + cos3x.sinx) – 2( sin² 3x+ cos² 3x) + cos3x = 0

⇒ sin4x –2 + cos3x= 0

⇒ sin4x+ cos3x = 2 (*)

Với mọi x ta có: - 1 ≤ sin4x ≤ 1 và-1 ≤ cos3x ≤ 1

⇒ - 2 ≤ sin4x+cos3x ≤ 2

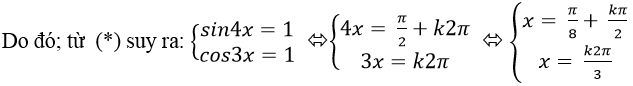
⇒ Không có giá trị nào của x thỏa mãn.

Vậy phương trình đã cho vô nghiệm

Chọn D

Ví dụ 5. Giải phương trình: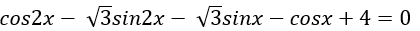

A.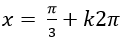

B.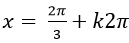

C.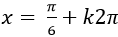

D.Vô nghiệm

Lời giải

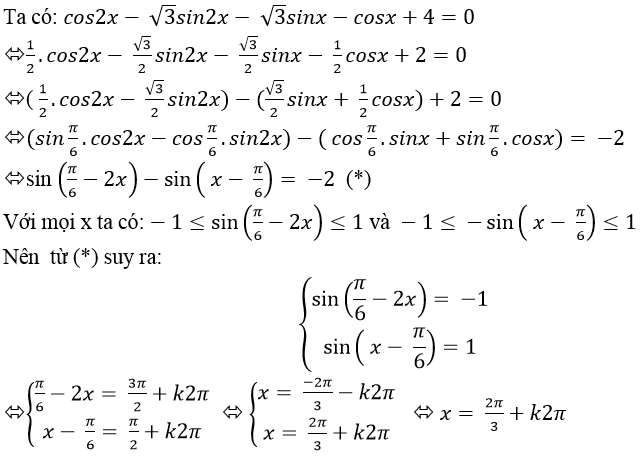
Chọn B.

Ví dụ 6. Giải phương trình sin²⁰x + cos²⁰ x= 1

A. x= kπ

B. x= kπ/2

C. x= π/2+kπ

D. x= kπ/4

Lời giaỉ

Ta có: sin²⁰ x + cos²⁰ x = 1

⇒ sin²⁰ x + cos²⁰ x = sin² x+ cos² x

⇒ sin²⁰ x - sin² x = cos² x- cos²⁰ x

⇒ sin² x( sin¹⁸ x – 1)= cos² x( 1- cos¹⁸ x)

+ Với mọi x ta luôn có: - 1 ≤ sinx ≤ 1 ⇒ 0 ≤ sin² x ≤ 1

⇒ sin¹⁸x- 1 < 0

⇒ vế trái ≤ 0 (1)

+ Tương tự có: 1- cos¹⁸x ≥ 0

⇒ Vế phải ≥ 0 (2)

Từ (1) và (2) suy ra: vế trái= vế phải = 0

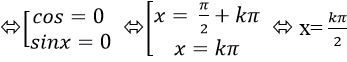
Vậy nghiệm phương trình đã cho là x= kπ/2

Chọn B.

Ví dụ 7. Giải phương trình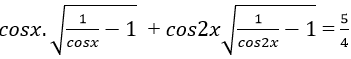

A. x= π/4+kπ

B. kπ

C. Vô nghiệm

D. Cả A và B đúng

Lời giải

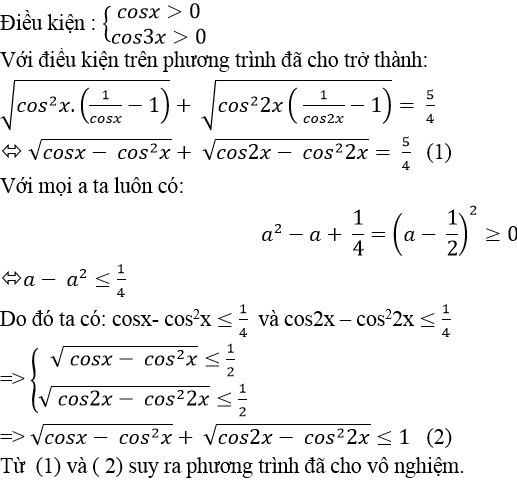
Chọn C.

Ví dụ 8. Giải phương trình: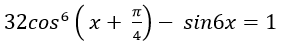

A.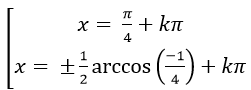

B.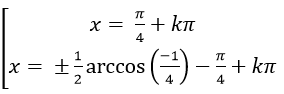

C.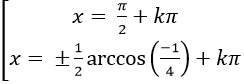

D. Phương trình vô nghiệm

Lời giải

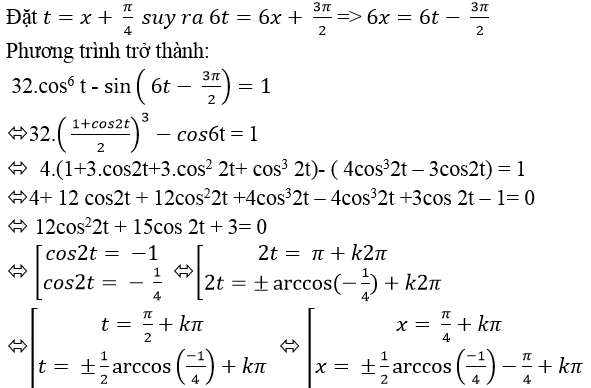
Chọn B .

Ví dụ 9. Giải phương trình: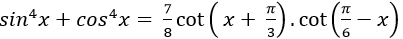

A.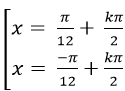

B.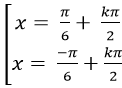

C.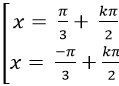

D. Đáp án khác

Lời giải

Chọn A.

Ví dụ 10. Giải phương trình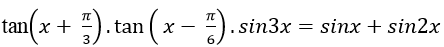

A.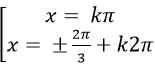

B.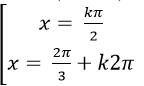

C.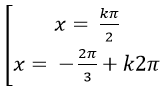

D.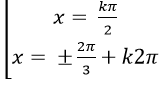

Lời giải

Chọn D.

Ví dụ 11. Cho phương trình: 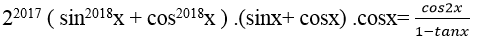Nghiệm dương nhỏ nhất của phương trình có dạng πa/b với a; b là các số nguyên và nguyên tố cùng nhau. Tính S= b-a

A. 2

B. 3

C. 4

D.1

Lời giải.

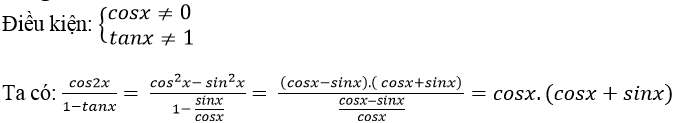
Do đó phương trình đã cho trở thành:

2²⁰¹⁷.( sin²⁰¹⁸x + cos²⁰¹⁸x ) .(sinx+ cosx) .cosx= cosx( sinx+ cosx)

⇒ 2²⁰¹⁷.( sin²⁰¹⁸x + cos²⁰¹⁸x ) .(sinx+ cosx) .cosx- cosx( sinx+ cosx) = 0

⇒ cosx.( cosx+ sinx) .[ 2²⁰¹⁷.( sin²⁰¹⁸x + cos²⁰¹⁸x )- 1] = 0

Chọn D.

Ví dụ 12. Giải phương trình :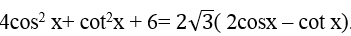

A.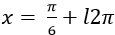

B.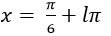

C.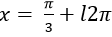

D.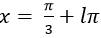

Lời giải

+ Điều kiện: sinx ≠ 0

Chọn A.

Ví dụ 13. Giải phương trình: sin3x. ( cosx- 2sin3x) + cos3x. (1+ sinx – 2cos3x) =0

A.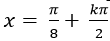

B.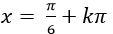

C.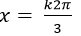

D. Vô nghiệm

Lời giải

Ta có: sin3x. ( cosx- 2sin3x) + cos3x. (1+ sinx – 2cos3x) = 0

⇒ sin3x. cosx – 2sin²3x + cos3x + cos3x.sinx – 2cos²3x=0

⇒ ( sin3x. cosx + cos3x. sinx) - 2( sin²3x + cos²3x) +cos3x = 0

⇒ sin4x - 2+ cos3x= 0

⇒ sin4x + cos3x = 2 (1)

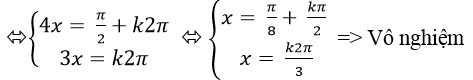
Vậy phương trình đã cho vô nghiệm.

Chọn D.

C. Bài tập vận dụng

Câu 1:Giải phương trình: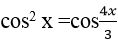

A.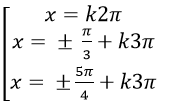

B.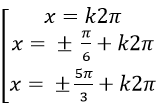

C.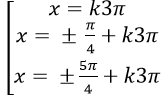

D. Đáp án khác

Lời giải:

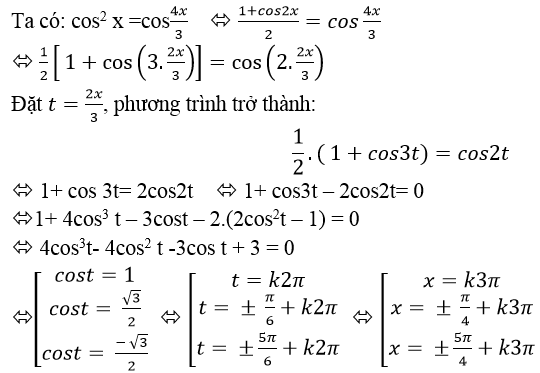
Chọn C.

Câu 2:Giải phương trình: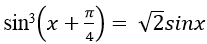

A.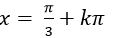

B.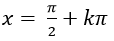

C.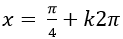

D.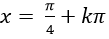

Lời giải:

Chọn D.

Câu 3:Giải phương trình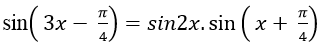

A.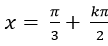

B.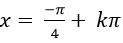

C.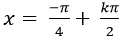

D.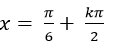

Lời giải:

Chọn C.

Câu 4:Giải phương trình: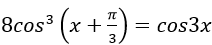

A.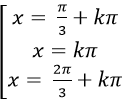

B.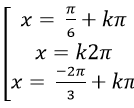

C.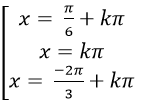

D.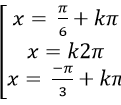

Lời giải:

Chọn C.

Câu 5:Giải phương trình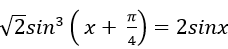

A.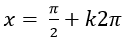

B.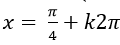

C.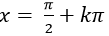

D.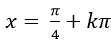

Lời giải:

Chọn D.

Câu 6:Giải phương trình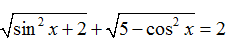

A.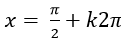

B.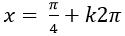

C.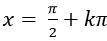

D.Vô nghiệm

Lời giải:

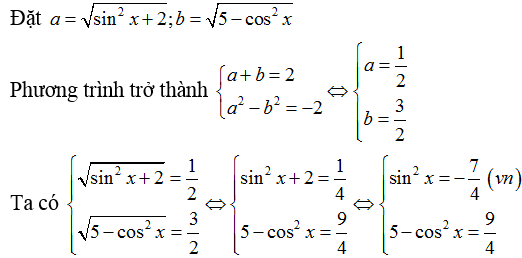
Vậy hệ phương trình đã cho vô nghiệm

Chọn D.

Câu 6:Giải phương trình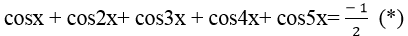

A.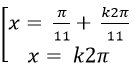

B.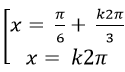

C.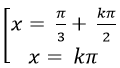

D.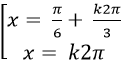

Lời giải:

+ Ta thấy khi sinx=0 ⇒ x= kπ không phải là nghiệm của phương trình.

+ Nhân hai vế của phương trình (*) với sinx ≠ 0 ta được:

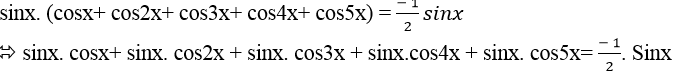
⇒ 2sinx. cosx+ 2sinx.cos2x+ 2sinx.cos3x + 2sinx. cos4x + 2sinx. cos5x + sinx=0

⇒ sin2x – sinx + sin3x- sin2x + sin4x- sin3x + sin5x- sin4x+ sin6x + sinx= 0

⇒ sin 5x+ sin 6x = 0

⇒ sin5x= - sin6x= sin( π-6x)

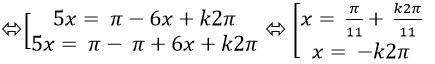
Chọn A.

Câu 7:Giải phương trình : 4sin3x. cos2x =1+ 6sinx – 8sin³ x

A.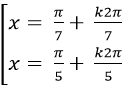

B.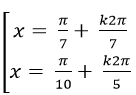

C.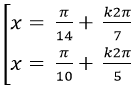

D.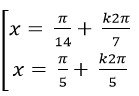

Lời giải:

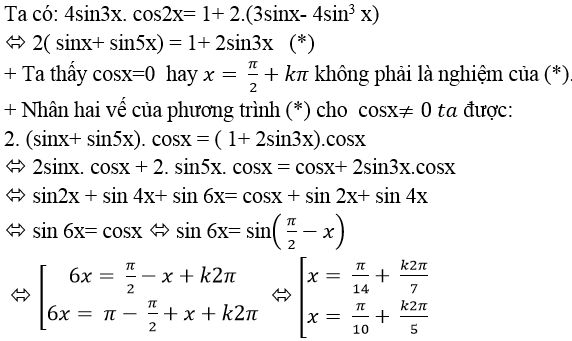
Chọn C.

Câu 8:Giải phương trình: cosx. cos2x. cos4x. cos 8x= 1/16 ( *)

A. x=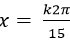

B. x=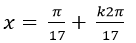

C. x=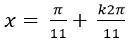

D. Đáp án khác

Lời giải:

+ Ta thấy khi sinx=0 hay x=kπ không phải là nghiệm của phương trình đã cho.

+ Nhân hai vế của phương trình (*) với sin x ≠ 0 ta được:

Chọn D.

Câu 9:Nghiệm dương nhỏ nhất của phương trình cos3x. (2cos2x+ 1) = 1/2 có dạng πa/b với a ; b là các số nguyên và nguyên tố cùng nhau. Tính S= a. b

A. 6

B.7

C. 8

D. 9

Lời giải:

Ta có: cos3x. (2cos2x+ 1) = 1/2

⇒ 4. cos3x. cos2x+ 2cos3x= 1

⇒ 2. ( cos5x+ cosx) + 2cos3x= 1

⇒ 2cos5x+ 2cosx+ 2cos3x=1

+ Nhận thấy sinx=0 hay x=kπ không thỏa mãn phương trình trên.

+ Nhân hai vế cho sinx ≠ 0 ta được:

2.sinx. cos5x+ 2. cosx. sinx + 2cos3x. sinx= sinx

⇒ sin6x + sin(-4x) + sin2x + sin 4x + sin( - 2x) = sinx

⇒ sin6x - sin 4x + sin2x+sin4x – sin2x- sinx=0

⇒ sin6x- sinx=0 ⇒ sin6x= sinx

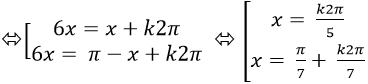
Suy ra nghiệm dương nhỏ nhất là π/7 ⇒ a= 1 và b= 7

⇒ S= a.b= 1.7= 7

Chọn B.

Câu 10:Cho phương trình sin²⁰¹⁸x + cos²⁰¹⁸x = 2( sin²⁰²⁰x+ cos²⁰²⁰x). Số vị trí biểu diễn các nghiệm của phương trình trên đường tròn lượng giác là

A. 3

B. 4

C. 6

D. 8

Lời giải:

Ta có: sin²⁰¹⁸x+ cos²⁰¹⁸ x= 2( sin²⁰²⁰x+ cos²⁰²⁰x)

⇒ ( sin²⁰¹⁸ x- 2sin²⁰²⁰ x) + (cos²⁰¹⁸ x- 2cos²⁰²⁰ x) = 0

⇒ sin²⁰¹⁸ x.(1 – 2sin² x) + cos²⁰¹⁸x. ( 1- 2cos² x) = 0

⇒ sin²⁰¹⁸ x.cos2x – cos²⁰¹⁸x. cos2x= 0

⇒ cos2x. ( sin²⁰¹⁸ x- cos²⁰¹⁸x)= 0

Chọn B.

Câu 11:Nghiệm dương lớn nhất của phương trình tan²⁰¹⁸ x+ cot²⁰¹⁸x = 2.sin²⁰¹⁷(x+ π/4) có dạng πa/b với a; b là các số nguyên a > 0 và a; b nguyên tố cùng nhau. Tính S= a.b

A. 4

B. 3

C. 6

D. 8

Lời giải:

⇒ nghiệm dương lớn nhất là x= π/4

⇒ a= 1 và b= 4 nên S=a.b = 4

Chọn A.

Câu 12:Giải phương trình:

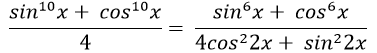
A. x= kπ/4

B. x= kπ/2

C. kπ

D. kπ/3

Lời giải:

+ Ta có: 4cos²2x + sin²2x = ( cos² 2x + sin²2x ) +3cos²2x

= 1+ 3cos²2x > 0 với mọi x.

⇒ Phương trình luôn xác định với mọi giá trị của x.

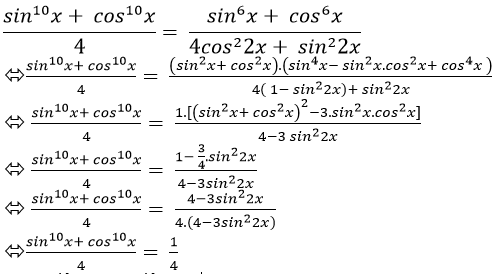
⇒ sin¹⁰x + cos¹⁰x = 1

⇒ sin¹⁰ x+ cos¹⁰ x= sin² x+ cos² x

⇒ (sin¹⁰ x- sin² x)+ ( cos10x – cos² x) = 0

⇒ sin² x(sin⁸x -1) + cos² x( cos⁸ x- 1) = 0 (*)

Với mọi ta có: - 1 ≤ sinx;cosx ≤ 1

⇒ sin⁸ x- 1 < 0 và cos⁸ x – 1 < 0 nên từ (*) suy ra:

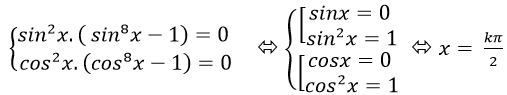
Chọn B.

Câu 13:Cho phương trình: 4cos²x+ tan² x+ 4= 2.(2cosx – tanx ) . Tìm số nghiệm của phương trình trên khoảng ( 0; 10π)?

A. 10

B.16

C. 22

D. Vô nghiệm

Lời giải:

Điều kiện: cosx ≠ 0 hay x ≠ π/2+kπ

Ta có: 4cos² x+ tan² x+ 4= 2.( 2cosx- tanx)

⇒ 4cos² x – 4cosx + 1+ tan²x + 2tanx + 1+ 2= 0

⇒ ( 2cosx-1)² + ( tanx+ 1)² + 2= 0

Với mọi x thỏa mãn điều kiện ta có: (2cosx -1)² ≥ 0 và ( tanx+ 1)² ≥ 0

⇒ ( 2cosx-1)² + ( tanx+ 1)² + 2 > 0

⇒ Phương trình đã cho vô nghiệm.

Chọn D.