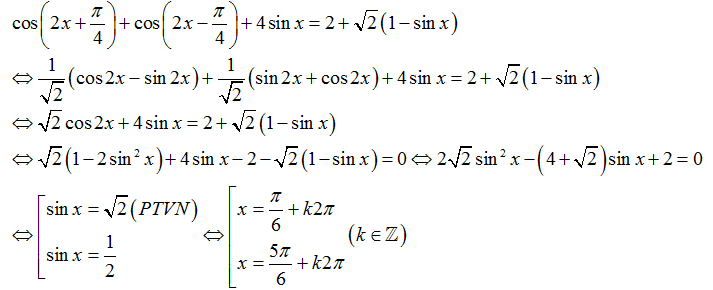Phương trình quy về phương trình bậc hai đối với hàm số lượng giác - Toán lớp 11

---

Phương trình quy về phương trình bậc hai đối với hàm số lượng giác

Với Phương trình quy về phương trình bậc hai đối với hàm số lượng giác Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương trình quy về phương trình bậc hai đối với hàm số lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

Để giải phương trình quy về phương trình phương trình bậc hai đối với một hàm số lượng giác.

• Sử dụng các công thức cộng; công thức nhân đôi; công thức biến đổi tổng thành tích; tích thành tổng. ..để đưa phương trình đã cho về phương trình bậc hai đối với một hàm số lượng giác.

• Sử dụng cách giải phương trình phương trình bậc hai đối với một hàm số lượng giác. Từ đó;suy ra nghiệm của phương trình đã cho.

B. Ví dụ minh họa

Ví dụ 1. Giải phương trình: cosx = 3 - sin² x

A. π+k2π

B. k2π

C. kπ

D. π/2+ k2π

Lời giải

Ta có: cosx = 3- sin² x

⇒ 3- sin² x – cosx= 0

⇒ 3- (1- cos² x ) – cosx= 0

⇒ cos² x- cosx + 2= 0

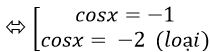
Với cosx= -1 thì x= π+k2π

Chọn A.

Ví dụ 2. Giải phương trình : sin² x+ 2sin² 2x – 6sinx. cosx+ cos²x = 0

A.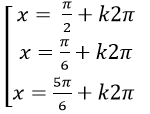

B.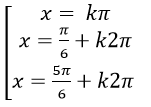

C.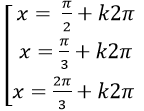

D.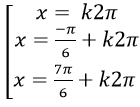

Lời giải

Ta có: sin²x+ 2sin² 2x – 6sinx. cosx+ cos²x = 0

⇒ 2sin²2x -6sinx.cosx + (sin² x+ cos²x ) = 0

⇒ 2sin² 2x – 3sin2x +1= 0

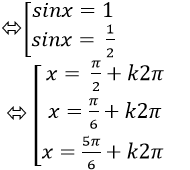
Chọn A.

Ví dụ 3. Giải phương trình: 2cos² x+ 5sin²x+ 5sinx= 0

A.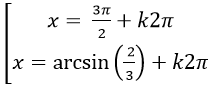

B.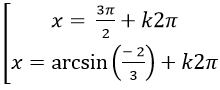

C.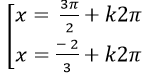

D. Đáp án khác

Lời giải

Ta có: 2cos² x+ 5sin² x+ 5sinx=0

⇒ 2( cos² x+ sin² x) + 3sin²x+ 5sinx = 0

⇒ 2+ 3sin² x+ 5sinx= 0

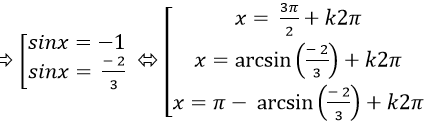
Chọn D.

Ví dụ 4. Các họ nghiệm của phương trình cos2x- sinx= 0 là

A.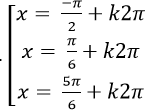

B.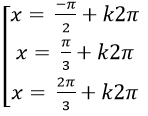

C.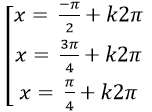

D.Đáp án khác

Lời giải

Ta có: cos2x- sinx=0

⇒ 1- 2sin² x – sinx= 0

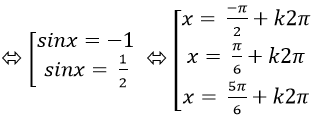
Chọn A.

Ví dụ 5. Họ nghiệm của phương trình – cos²2x – 2sin2x + 2= 0 là :

A.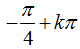

B.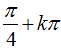

C.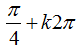

D.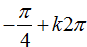

Lời giải

Ta có: - cos² 2x – 2sin2x+ 2 = 0

⇒ sin² 2x- 1- 2sin2x + 2= 0

⇒ sin² 2x – 2sin2x +1=0

⇒ sin2x= 1

⇒ 2x= π/2+k2π ⇒ x= π/4+kπ

Chọn B.

Ví dụ 6: Một họ nghiệm của phương trình cos²2x + sin2x- 1= 0 là

A.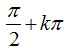

B.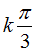

C.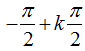

D.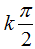

Lời giải

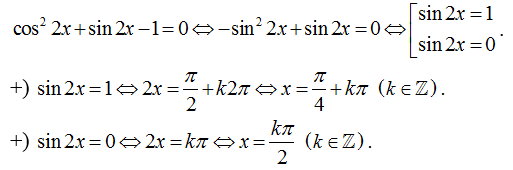
Chọn D.

Ví dụ 7. Giải phương trình lượng giác 4sin⁴x +12cos² x – 7= 0 có nghiệm là:

A.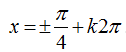

B.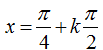

C.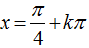

D.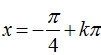

Lời giải

Ta có: 4sin²x +12cos² x – 7= 0

⇒ 4sin² x + 12(1-sin² x) – 7 = 0

⇒ 4sin² x – 12sin²x + 5= 0 .

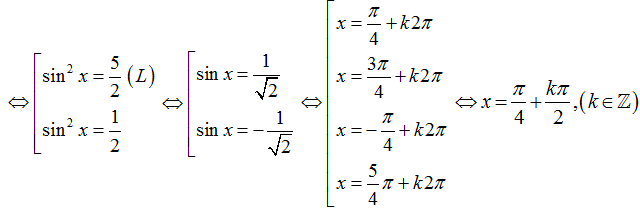
Chọn B.

Ví dụ 8: Phương trình cos2(x+ π/3)+4 cos⁡(π/6-x)= 5/2 có nghiệm là:

A.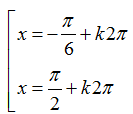

B.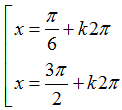

C.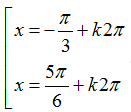

D.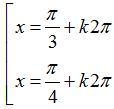

Lời giải

Ta có:

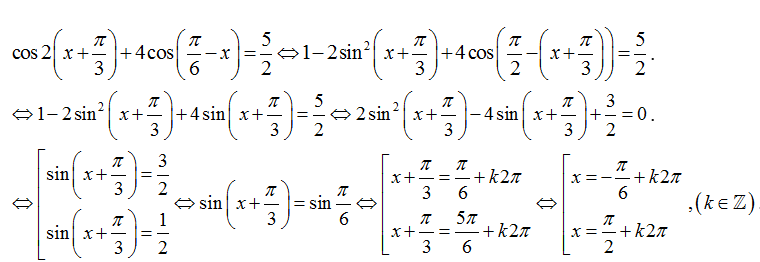
Chọn A.

Ví dụ 9. Phương trình cos2x - 10cosx + 13= 0 có nghiệm là:

A. x= π/2+k2π

B.Ø .

C. x = ±arccos 2 + k2π.

D. x = ±arccos 3 + k2π.

Lời giải

Ta có: cos2x- 10cosx + 13= 0

⇒ 2cos² x – 1- 10cosx + 13= 0

⇒ 2cos² x – 10cosx + 12= 0

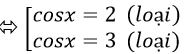
⇒ Phương trình đã cho vô nghiệm.

Chọn B.

Ví dụ 10: Phương trình sin²2x- 2cos² x+ 3/4=0 có nghiệm là

A.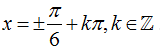

B.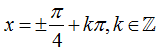

C.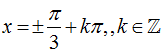

D.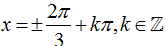

Lời giải

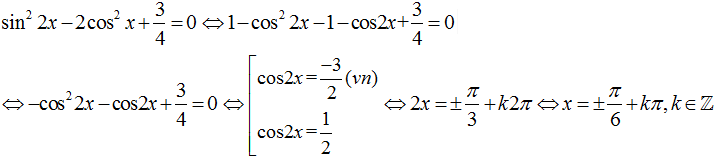
Chọn A.

Ví dụ 11: Họ nghiệm của phương trình 3cos 4x + 2cos2x- 5= 0 là

A.k2π

B. π/3+ k2π.

C.kπ

D. π/3+ k2π.

Lời giải

Ta có: 3cos4x + 2cos2x – 5 = 0

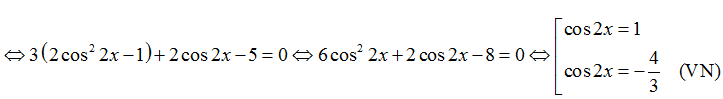
Với cos2x= 1 thì 2x= k2π ⇒ x= k.π

Chọn C.

Ví dụ 12. Giải phương trình: .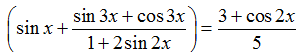

A.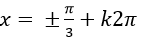

B.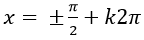

C.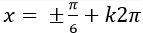

D. Đáp án khác

Lời giải

C. Bài tập vận dụng

Câu 1:Câu 1: Phương trình sin² x+ sin² 2x = 1 có nghiệm là:

A.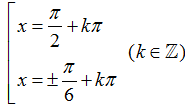

B.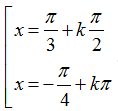

C.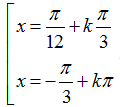

D. Vô nghiệm.

Lời giải:

Ta có: sin² x+ sin² 2x = 1

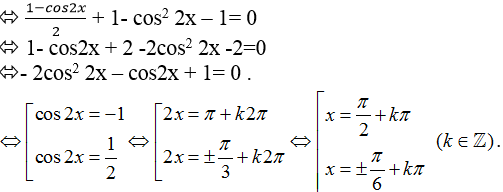
Câu 2:Phương trình tanx + 3cotx = 4 có nghiệm là:

A.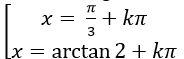

B.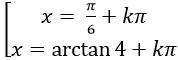

C.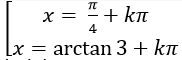

D.Đáp án khác

Lời giải:

Điều kiện: x ≠ kπ

Ta có: tanx+ 3cotx = 4

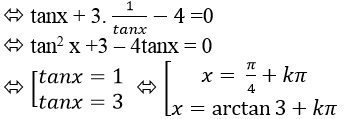
Chọn C.

Câu 3:Phương trình 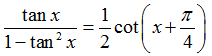có mấy họ nghiệm :

A. 0

B.1

C. 2

D. 3

Lời giải:

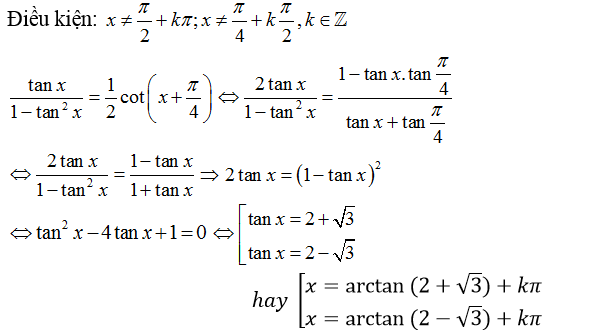
Vậy phương trình đã cho có hai họ nghiệm.

Chọn C.

Câu 4:Phương trình 2√2 ( sinx+cosx).cosx=3+cos2x có nghiệm là:

A.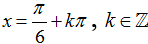

B.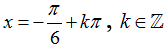

C.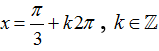

D. Vô nghiệm.

Lời giải:

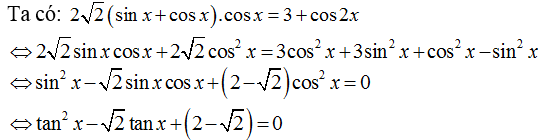
(vì cosx = 0 không là nghiệm của phương trình nên ta chia cả hai vế của phương trình cho cos² x)

Phương trình vô nghiệm.

Chọn D.

Câu 5:Giải phương trình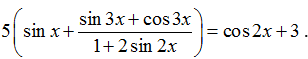

A.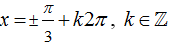

B.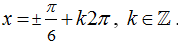

C.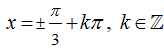

D.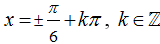

Lời giải:

Chọn A.

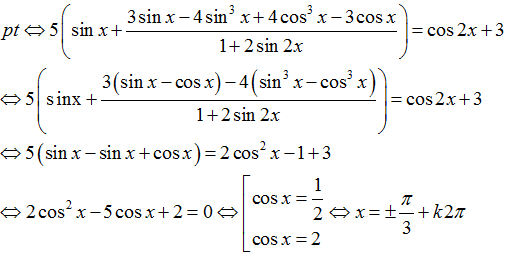
Câu 6:Phương trình: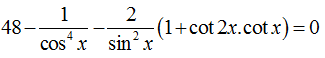 có các nghiệm là

A.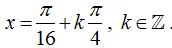

B.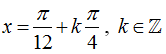

C.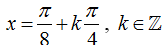

D.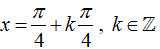

Lời giải:

Chọn C

Câu 7:Phương trình cos2x + sin² x+ 2cosx + 1= 0 có nghiệm là

A.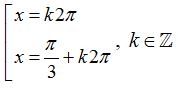

B.π+k2π

C.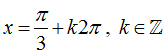

D.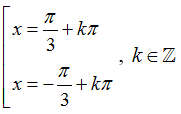

Lời giải:

Chọn B

Ta có: cos2x + sin² x+ 2cosx + 1= 0

⇒ 2 cos² x- 1+ 1- cos² x+ 2cosx+1= 0

⇒ cos²x + 2cosx+1 =0 ⇒ cosx=-1 ⇒ x= π+k2π, k nguyên.

Câu 8:Phương trình: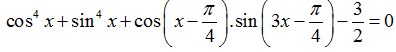 có nghiệm là:

A.k2π , k nguyên .

B.k3π , k nguyên .

C.k4π , k nguyên .

D.π/4 + kπ , k nguyên .

Lời giải:

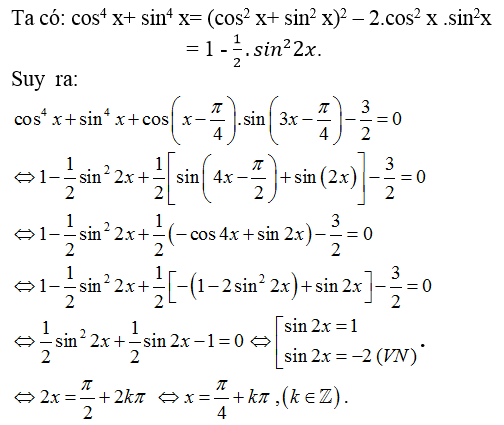
Chọn D.

Câu 9:Giải phương trình sin3x+ cos2x= 1+ 2sinx.cos2x

A.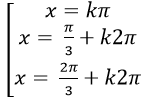

B.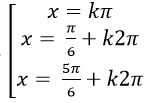

C.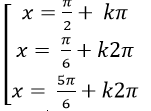

D. Đáp án khác

Lời giải:

Chọn B.

Phương trình sin3x+ cos2x = 1+ 2sinx.cos2x

⇒ sin3x +cos2x = 1+ sin3x + sin(-x)

⇒ cos2x–1-sin(-x) = 0

⇒ 1- 2sin2 x- 1 + sinx= 0

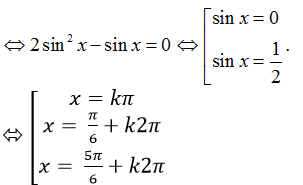
Câu 10:Số họ nghiệm của phương trình cos5x+ cos2x+2sin3x.sin2x=0 là

A. 1

B. 2

C. 3

D. 4

Lời giải:

Ta có: cos5x+ cos2x + 2sin3x. sin2x= 0

⇒ cos 5x+ cos 2x – cos 5x+ cosx= 0

⇒ cos2x + cosx= 0

⇒ 2cos² x- 1+ cosx= 0

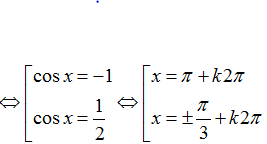
Vậy phương trình đã cho có 3 họ nghiệm.

Chọn C

Câu 11:Tìm nghiệm của phương trình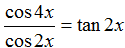

A.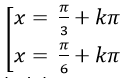

B.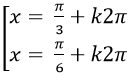

C.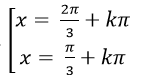

D. Đáp án khác

Lời giải:

Chọn A

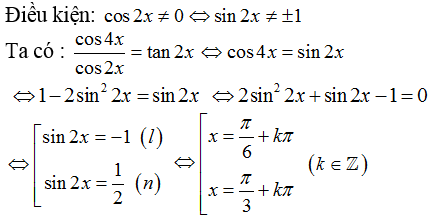
Câu 12:Nghiệm phương trình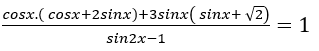

A.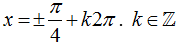

B.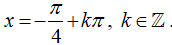

C.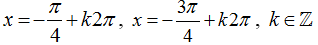

D.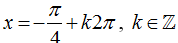

Lời giải:

Chọn D.

Câu 13:Cho phương trình cos5x.cosx= cos4x.cos2x + 3cos² x+ 1. Các nghiệm thuộc khoảng của phương trình là:

A.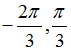

B.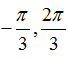

C.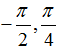

D.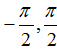

Lời giải:

Ta có: cos 5x.cosx= cos4x. cos2x + 3cos2 x+ 1

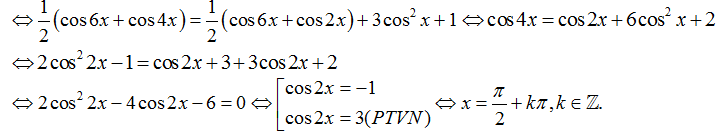
Vậy các nghiệm thuộc khoảng (-π;π) của phương trình là x= -π/2; x= π/2

Chọn D

Câu 14:Phương trình: 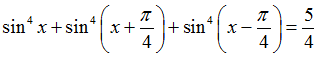có nghiệm là:

A.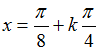

B.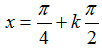

C.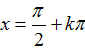

D.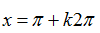

Lời giải:

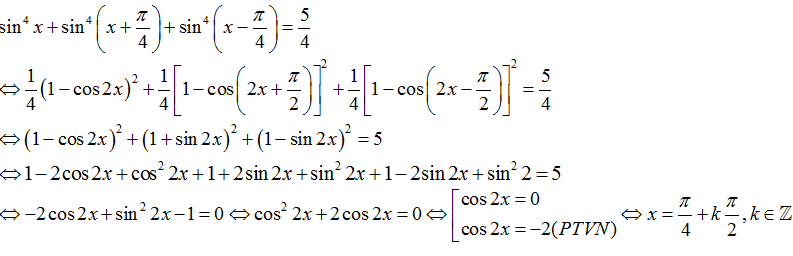
Chọn B.

Câu 15: Phương trình: 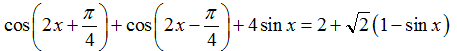có nghiệm là:

A.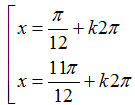

B.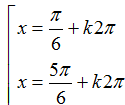

C.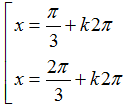

D.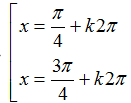

Lời giải:

Chọn B.