Tìm ảnh của một đường tròn qua phép đối xứng trục cực hay - Toán lớp 11
Tìm ảnh của một đường tròn qua phép đối xứng trục cực hay
Với Tìm ảnh của một đường tròn qua phép đối xứng trục cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm ảnh của một đường tròn qua phép đối xứng trục từ đó đạt điểm cao trong bài thi môn Toán lớp 11.
A. Phương pháp giải
Phép đối xứng trục biến một đường tròn thành đường tròn có cùng bán kính
Cách 1.
Bước 1: Tìm ảnh I’ của âm I là tâm của đường tròn (C) qua phép đối xứng trục.
Bước 2: Viết phương trình đường tròn (C’) với tâm I’ và bán kính R’ = R.
Cách 2. Sử dụng biểu thức tọa độ với trường hợp trục đối xứng là Ox hoặc Oy
B. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng tọa độ Oxy cho đường tròn (C): (x - 3)2 + (y + 5)2 = 36. Viết phương trình đường tròn (C') là ảnh của (C) qua phép đối xứng trục Ox
Hướng dẫn giải:
Cách 1. Đường tròn (C) có tâm I(3;-5) và bán kính R = 6
Ta có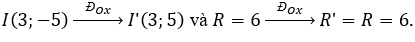 
Do đó (C') có phương trình (x - 3)2 + (y - 5)2 = 36.
Cách 2. Biểu thức tọa độ qua phép đối xứng trục Ox là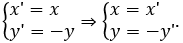 
Thay vào (C), ta được (x' - 3)2 + (-y' + 5)2 = 36 hay (x' - 3)2 + (y' - 5)2 =36.
Vậy (C') có phương trình (x - 3)2 + (y - 5)2 = 36.
Ví dụ 2: Trong mặt phẳng tọa độ Oxy, cho đường tròn(C): (x - 2)2 + (y + 5)2 = 16. Viết phương trình đường tròn (C')là ảnh của đường tròn (C) qua phép đối xứng trục Oy.
Hướng dẫn giải:
Đường tròn có tâm I(2;-5); bán kính R = 4.
Ảnh của tâm I(2;-5) qua trục Oylà I'(-2;-5).
Do đó ảnh của đường tròn qua trục Oylà (C'): (x + 2)2 + (y + 5)2 = 16.
Ví dụ 3: Cho đường tròn (C): x2 + y2 -4x + 2y + 1 = 0 và đường thẳng d: 2x - y + 2 = 0. Hãy viết phương trình của đường tròn (C’) là ảnh của (C) qua phép đối xứng trục d.
Hướng dẫn giải:
Đường tròn (C) có tâm I(2;-1) và bán kính R = 2.
Gọi Hlà hình chiếu vuông góc của I lên d ⇒ IH ⊥ d ⇒ IH: x + 2y + c = 0.
I(2;-1) ∈ IH ⇒ 2 + 2.(-1) + c = 0 ⇒ c = 0 ⇒ IH: x + 2y = 0.
Gọi H=Δ∩d khi đó H là nghiệm của hệ:
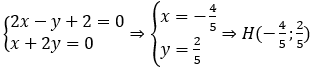
- Gọi I’(x;y) là tâm của (C’).Khi đó H là trung điểm của II’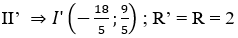 
- Vậy (C’):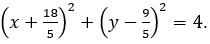 
C. Bài tập trắc nghiệm
Câu 1. Trong mặt phẳng tọa độ Oxy cho đường tròn (C): (x - 1)2 + (y + 2)2 = 4. Phép đối xứng trục Ox biến đường tròn (C) thành đường tròn (C') có phương trình là:
A. (x + 1)2 + (y - 2)2 = 4.
B. (x - 1)2 + (y + 2)2 = 4.
C. (x - 1)2 + (y - 2)2 = 4.
D. (x + 1)2 + (y + 2)2 = 4.
Lời giải:
.
Đường tròn (C) có tâm I(1;-2) và bán kính R = 2.
Ta có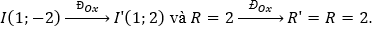 
Do đó (C') có phương trình (x - 1)2 + (y - 2)2 = 4.
Chọn C.
Cách 2. Biểu thức tọa độ qua phép đối xứng trục Ox là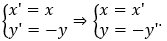 
Thay vào (C), ta được (x' - 1)2 + (-y' + 2)2 = 4 hay (x' - 1)2 + (y' - 2)2 = 4.
Câu 2. Trong mặt phẳng Oxy, cho đường thẳng đường tròn (C): x2 + y2 + 2x - 4y-4 = 0. Tìm ảnh của (C)qua phép đối xứng trục Ox.
A. (C'): (x + 2)2 + (y + 2)2 = 9
B. (C'): (x + 1)2 + (y + 1)2 = 9
C. (C'): (x + 3)2 + (y + 2)2 = 9
D. (C'): (x + 1)2 + (y + 2)2 = 9
Lời giải:
.
Chọn D.
Cách 1: Ta thấy (C) có tâm I(-1;2) và bán kính R = 3.
Gọi I',R' là tâm và bán kính của (C')thì I'(-1;-2) và R' = R = 3, do đó (C'): (x + 1)2 + (y + 2)2 = 9.
Cách 2: Lấy P(x;y) ∈ (C) ⇒ x2 + y2 + 2x - 4y - 4 = 0 (2).
Gọi Q(x';y') là ảnh của P qua phép đối xứng ĐOx. Ta có
thay vào (2) ta được x'2 + y'2 + 2x' + 4y' - 4 = 0, hay (C'): x2 + y2 + 2x + 4y - 4 = 0.
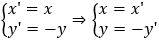
Câu 3. Trong mặt phẳng tọa độ Oxy, cho đường tròn(C): (x - 2)2 + (y + 3)2 = 9. Viết phương trình đường tròn (C')là ảnh của đường tròn (C) qua phép đối xứng trục Oy.
A. (C'): (x + 2)2 + (y + 3)2 = 9.
B. (C'): (x - 2)2 + (y - 3)2 = 9.
C. (C'): (x - 2)2 + (y + 2)2 = 9.
D. (C'): (x + 2)2 + (y + 3)2 = 4.
Lời giải:
Chọn A
Đường tròn có tâm I(2;-3); bán kính R = 3.
Ảnh của tâm I(2;-3) qua trục Oylà I'(-2;-3).
Do đó ảnh của đường tròn qua trục Oylà (C'): (x + 2)2 + (y + 3)2 = 9.
Câu 4. Trong mặt phẳng tọa độ Oxy, cho đường tròn(C): (x - 7)2 + (y + 5)2 = 25. Viết phương trình đường tròn (C')là ảnh của đường tròn (C) qua phép đối xứng trục Oy.
A. (C'): (x + 7)2 + (y - 5)2 = 25.
B. (C'): (x + 7)2 + (y + 5)2 = 25.
C. (C'): (x - 7)2 + (y + 5)2 = 25.
D. (C'): (x + 7)2 + (y + 5)2 =5.
Lời giải:
Chọn B
Đường tròn có tâm I(7;-5); bán kính R = 5.
Ảnh của tâm I(7;-5) qua trục Oylà I'(-7;-5).
Do đó ảnh của đường tròn qua trục Oylà (C'): (x + 7)2 + (y + 5)2 = 25.
Câu 5. Trong mặt phẳng tọa độ Oxy cho đường tròn (C): (x + 1)2 + (y - 4)2 = 1 và đường thẳng d có phương trình y - x = 0. Phép đối xứng trục d biến đường tròn (C) thành đường tròn (C') có phương trình là:
A. (x + 1)2 + (y - 4)2 = 1.
B. (x - 4)2 + (y + 1)2 = 1.
C. (x + 4)2 + (y - 1)2 = 1.
D. (x + 4)2 + (y + 1)2 = 1.
Lời giải:
.
Biểu thức tọa độ của phép đối xứng qua trục d:y-x = 0 là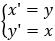 
. Thay vào (C), ta được (y' + 1)2 + (x' - 4)2 = 1 hay (x - 4)2 + (y + 1)2 = 1.
Chọn B.
Câu 6. Cho đường tròn (C): (x - 1)2 + (y + 1)2 = 4.
Tìm ảnh của (C) qua phép đối xứng trục d: x + y - 2 = 0
A. (C'): (x - 2)2 + (y - 1)2 = 4
B. (C'): (x - 3)2 + (y - 3)2 = 4
C. (C'): (x - 3)2 + (y - 2)2 = 4
D. (C'): (x - 3)2 + (y - 1)2 = 4
Lời giải:
Chọn D.
Đường tròn (C) có tâm I(1;-1) và bán kính R = 2.
Gọi H là hình chiếu vuông góc của I lên d ⇒ IH⊥d ⇒ IH: x - y + c = 0.
I(1;-1) ∈ IH ⇒ 1 - (-1) + c = 0 ⇒ c = -2
⇒ IH: x - y - 2 = 0
Vì H = MH ∩ d thì tọa độ của điểm H là nghiệm của hệ:
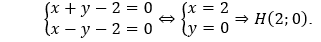
Gọi I' = Đd (I) thì H là trung điểm của II' nên suy tra I'(3;1)
Đường tròn (C') có tâm I(3;1) và bán kính R' = R = 2 có phương trình: (C'): (x - 3)2 + (y - 1)2 = 4
Câu 7. Trong mặt phẳng tọa độ Oxy cho hai đường tròn (C): (x - 1)2 + (y - 2)2 = 4 và (C'): (x - 3)2 + y2 = 4. Viết phương trình trục đối xứng của (C) và (C').
A. y = x + 1.
B. y = x - 1.
C. y = -x + 1.
D. y = -x - 1.
Lời giải:
.
• Đường tròn (C) có tâm I (1;2); đường tròn (C’) có tâm I’(3;0).
• Trục đối xứng của hai đường tròn là trung trực của II’
• Gọi d là trục đối xứng cần tìm. Khi đó d đi qua trung điểm J(2;1) của đoạn thẳng II’ và nhận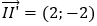 
làm véc tơ pháp tuyến nên có phương trình: 2(x - 2) - 2(y - 1) = 0 ⇔ 2x - 2y - 2 = 0 ⇔ x - y - 1 = 0
Vậy d: x - y - 1 = 0 ⇔ y = x - 1.
Chọn B.
Câu 8. Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?
A. Không có.
B. Một.
C. Hai.
D. Vô số
Lời giải:
Chọn B
Một đường tròn có vô số trục đối xứng đi qua tâm của đường tròn đó.
Vậy: Trục đối xứng thỏa yêu cầu của bài toán là đường thẳng nối hai tâm của đường tròn đã cho.
