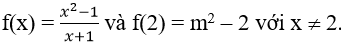Cách tìm m để hàm số liên tục cực hay - Toán lớp 11
Cách tìm m để hàm số liên tục cực hay
Với Cách tìm m để hàm số liên tục cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm m để hàm số liên tục từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải & Ví dụ
Ta sử dụng điều kiện để hàm số liên tục và điều kiện để phương trình có nghiệm để làm các bài toán dạng này.
- Điệu kiện để hàm số liên tục tại x0:
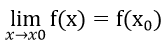
- Điều kiện để hàm số liên tục trên một tập D là f(x) liên tục tại mọi điểm thuộc D.
- Phương trình f(x) = 0 có ít nhất một nghiệm trên D nếu hàm số y = f(x) liên tục trên D và có hai số a, b thuộc D sao cho f(a).f(b) < 0.
Phương trình f(x) = 0 có k nghiệm trên D nếu hàm số y = f(x) liên tục trên D và tồn tại k khoảng rời nhau (ai ; ai+1) (i = 1,2,…,k) nằm trong D sao cho f(ai).f(ai+1) < 0.
Ví dụ minh họa
Bài 1: Xác định a để hàm số 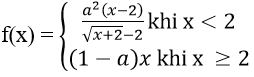
Hướng dẫn:
Hàm số xác định trên R
Với x < 2 ⇒ hàm số liên tục
Với x > 2 ⇒ hàm số liên tục
Với x = 2 ta có
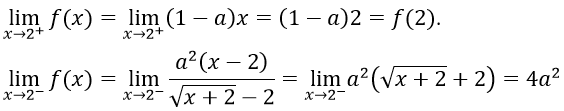
Hàm số liên tục trên R ⇔ hàm số liên tục tại x = 2
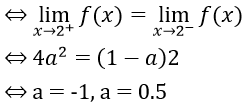
Vậy a = -1, a = 0.5 là những giá trị cần tìm.
Bài 2: Cho hàm số f(x) = x3 – 1000x2 + 0,01 . phương trình f(x) = 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây ?
I. (–1; 0) II. (0; 1) III. (1; 2)
Hướng dẫn:
Ta có hàm số y = f(x) = x3 – 1000x2 + 0,01 là hàm liên tục trên R
f(0) = 0.01 và f(-1) = - 1001 + 0.01 < 0. Nên f(0).(-1) < 0.
Vậy hàm số có nghiệm trong khoảng I
Bài 3: Tìm m để các hàm số sau liên tục trên R
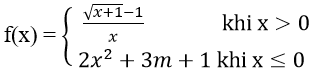
Hướng dẫn:
Với x < 0 ⇒ hàm số liên tục
Với x > 0 ⇒ hàm số liên tục
Với x = 0 ta có
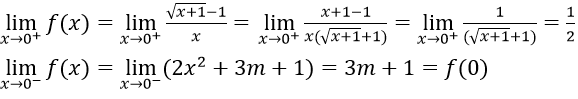
Hàm số liên tục trên R ⇔ hàm số liên tục tại x = 0
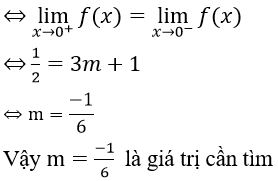
Bài 4: Chứng minh rằng phương trình sau có ít nhất một nghiệm :
x7 + 3x5 - 1 = 0
Hướng dẫn:
Ta có hàm số f(x) = x7 + 3x5 - 1 liên tục trên R và f(0).f(1) = - 3 < 0
Suy ra phương trinh f(x) = 0 có ít nhất một nghiệm thuộc (0,1).
Bài 5: Chứng minh rằng phương trình sau có ít nhất một nghiệm :
x2sinx + xcosx + 1 = 0
Hướng dẫn:
Ta có hàm số f(x) = x2sinx + xcosx + 1 liên tục trên R và f(0).f(π) = -π < 0. Suy ra phương trinh f(x) = 0 có ít nhất một nghiệm thuộc (0 ; π).
Bài 6: Xác định a, b để các hàm số sau liên tục trên R
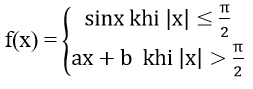
Hướng dẫn:
Ta có hàm số đã cho liên tục trên R\{π/2} do các hàm y = sinx và y = ax + b lên tục trên R.
Ta chỉ cần xét tính liên tục của hàm số tại x = π/2.
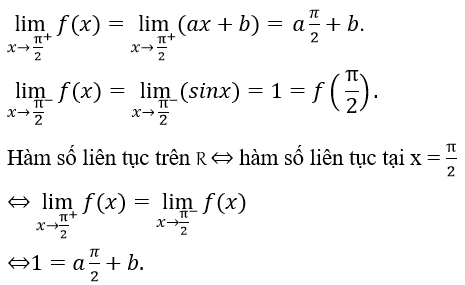
Vậy a, b là số thực thỏa mãn phương trình 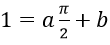
Bài 7: Tìm m để các hàm số sau liên tục trên R
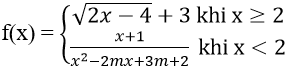
Hướng dẫn:
Hàm số xác định trên R
Với x < 2 ⇒ hàm số liên tục
Với x > 2 ⇒ hàm số liên tục
Với x = 2 ta có
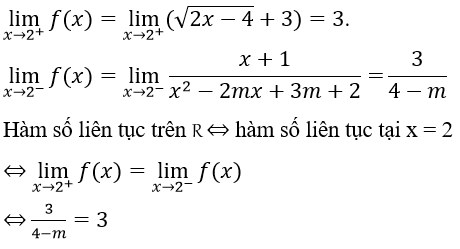
⇔ m = 3
Vậy m = 3 là giá trị cần tìm
Bài 8: Xác định a,b để các hàm số sau liên tục trên R
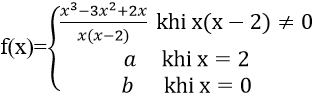
Hướng dẫn:
Với x ≠ 2 và x ≠ 0 hàm số liên tục.
Để hàm số đã cho liên tục trên R thì hàm số phải liên tục tại x = 2 và x = 0
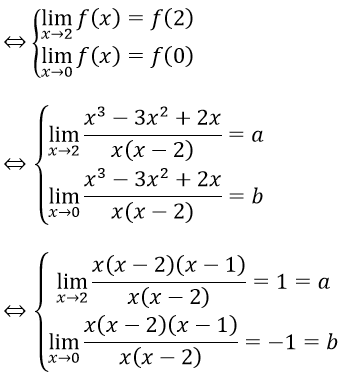
Vậy a = 1 và b = -1 thì hàm số liên tục trên R

B. Bài tập vận dụng
Bài 1: Cho hàm số:
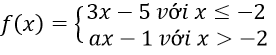
Với giá trị nào của a thì hàm số f(x) liên tục tại x = - 2?
A. a = -5
B. a = 0
C. a = 5
D. a = 6
Lời giải:
Đáp án: C
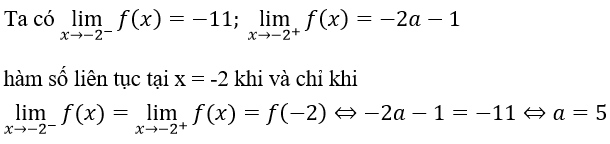
Đáp án C
Bài 2: Cho hàm số:
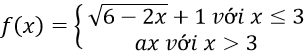
Với giá trị nào của a thì hàm số f(x) liên tục tại x = 3?
A. a = 3 B. a = 1/3 C. a = -1/3 C. a = -2
Lời giải:
Đáp án: B

Đáp án B
Bài 3: Cho hàm số:
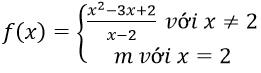
Với giá trị nào của m thì hàm số đã cho liên tục tại x = 2?
A. -2
B. -1
C. 1
D. 3
Lời giải:
Đáp án: C
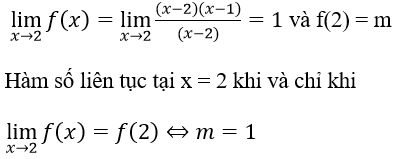
Đáp án C
Bài 4: Cho hàm số:
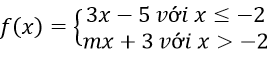
Giá trị nào của m để hàm số đã cho liên tục tại x = -2?
A. 7
B. -7
C. 5
D. 1
Lời giải:
Đáp án: A
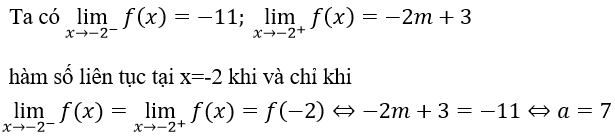
Đáp án A
Bài 5: Cho hàm số:
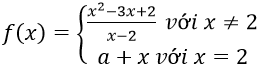
Với giá trị nào của a thì hàm số đã cho liên tục tại x = 2?
A. -2
B. -1
C. 1
D. 3
Lời giải:
Đáp án: B
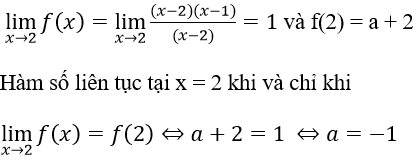
Đáp án B
Bài 6: Cho hàm số:
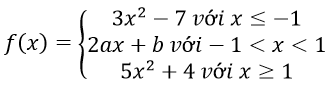
Hàm số đã cho liên tục trên R khi và chỉ khi:
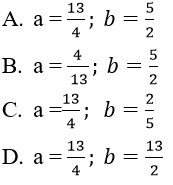
Lời giải:
Đáp án: A
Hàm số đã cho liên tục trên R khi và chỉ khi hàm số đó liên tục tại x = 1 và x = -1
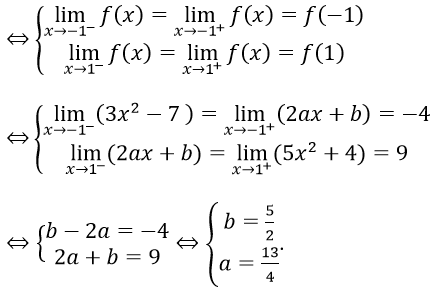
Đáp án A
Bài 7: Cho hàm số
Giá trị của m để f(x) liên tục tại x = 2 là:

Lời giải:
Đáp án: C
Hàm số liên tục tại x = 2 khi và chỉ khi
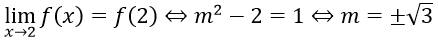
Đáp án C

Bài 8: Cho hàm số:
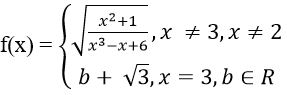
Tìm b để f(x) liên tục tại x = 3
A. √3 B. - √3 C. (2√3)/3 D. – (2√3)/3
Lời giải:
Đáp án: D
Hàm số liên tục tại x = 3 khi và chỉ khi
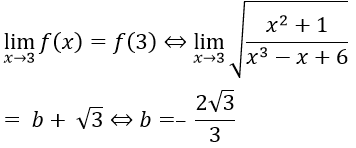
Đáp án D
Bài 9: Cho hàm số:
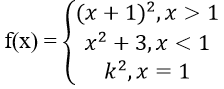
Tìm k để f(x) gián đoạn tại x = 1.

Lời giải:
Đáp án: A
f(x) gián đoạn tại x = 1 khi và chỉ khi:
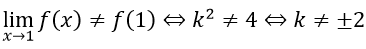
Đáp án A
Bài 10: Cho hàm số:
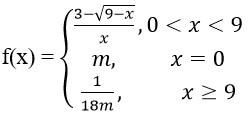
Tìm m để f(x) liên tục trên [0;+∞) là.
A.1/3 B. 1/2 C. 1/6 D. 1
Lời giải:
Đáp án: C
f(x) liên tục trên [0;+∞) khi và chỉ khi f(x) liên tục tại x = 0+ và liên tục tại x = 9
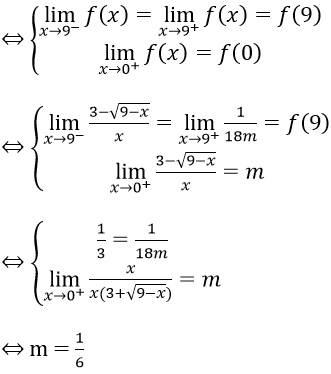
Đáp án C
Bài 11: Cho hàm số:
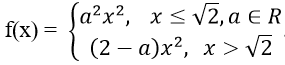
Giá trị của a để f(x) liên tục trên R là:
A. 1 và 2 B. 1 và –1 C. –1 và 2 D. 1 và –2
Lời giải:
Đáp án: D
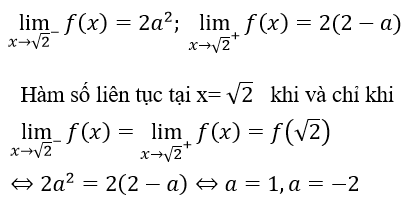
Đáp án D
Bài 12: Cho hàm số:
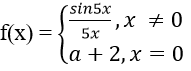
Tìm a để f(x) liên tục tại x = 0
A. 1 B. –1 C. –2 D. 2
Lời giải:
Đáp án: B
Hàm số liên tục tại x = khi và chỉ khi
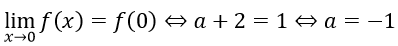
Đáp án B
Bài 13: Tìm khẳng định đúng trong các khẳng định sau:
I. f(x) liên tục trên đoạn [a;b] và f(a).f(b) > 0 thì tồn tại ít nhất số c ∈ (a;b) sao cho f(c) = 0
II. f(x) liên tục trên (a;b] và trên [b;c) nhưng không liên tục trên (a;c)
A. Chỉ I đúng B. Chỉ II đúng C. Cả I và II đúng D. Cả I và II sai
Lời giải:
Đáp án: D
Đáp án D
Bài 14: Tìm khẳng định đúng trong các khẳng định sau:
I. f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0 thì phương trình f(x) = 0 có nghiệm
II. f(x) không liên tục trên [a;b] và f(a).f(b) ≥ 0 thì phương trình f(x) = 0 vô nghiệm
A. Chỉ I đúng B. Chỉ II đúng C. Cả I và II đúng D. Cả I và II sai
Lời giải:
Đáp án: A
Đáp án A
Bài 15: Cho hàm số 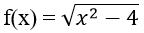
(I) f(x) liên tục tại x = 2
(II) f(x) gián đoạn tại x = 2
(III) f(x) liên tục trên đoạn [-2, 2]
A. Chỉ (I) và (III) B. Chỉ (I) C. Chỉ (II) D. Chỉ (II) và (III)
Lời giải:
Đáp án: B
TXĐ: D = (-∞, -2] ∪ [2, +∞). Vậy (III) và (II) sai. Đáp án B