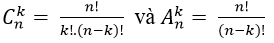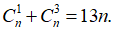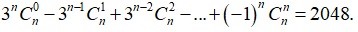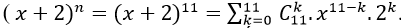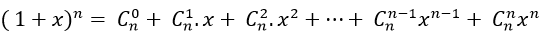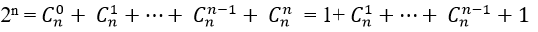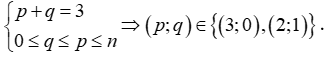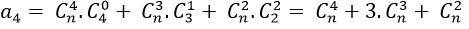Tìm số hạng chứa x^a trong khai triển đa thức P cực hay có lời giải - Toán lớp 11

---

Tìm số hạng chứa x^a trong khai triển đa thức P cực hay có lời giải

Với Tìm số hạng chứa x^a trong khai triển đa thức P cực hay có lời giải Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm số hạng chứa x^a trong khai triển đa thức P từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

+ Bước 1. Giải phương trình tổ hợp; chỉnh hợp để tìm n.( xuất phát từ đẳng thức chứa n) + Bước 2. Khai triển nhị thức New ton; tìm hệ số, số hạng thỏa mãn điều kiện đầu bài.

Chú ý :

B. Ví dụ minh họa

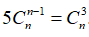
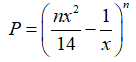
Ví dụ 1: Cho n là số dương thỏa mãn .Số hạng chứa x⁵ trong khai triển nhị thức Newton với x≠0 là

Hướng dẫn giải :

Đáp án : C

Ví dụ 2: Tìm số tự nhiên n; biết hệ số của số hạng thứ 3 theo số mũ giảm dần của x trong khai triển 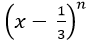bằng 4.

A.n = 6    B.n = 8    C.n = 9    D.n = 7

Hướng dẫn giải :

Đáp án :

Ví dụ 3: Tìm số hạng không chứa x trong khai triển biết 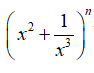là số nguyên dương thỏa mãn

A.160    B.240    C.180    D.210

Hướng dẫn giải :

Đáp án : D

Ví dụ 4: Tổng các hệ số nhị thức Niu – tơn trong khai triển (1+ x)³ⁿ bằng 64. Số hạng không chứa x trong khai triển ( 2nx+ 1/(2nx² ))³ⁿ là:

A.240    B.210    C.250    D.360

Hướng dẫn giải :

Đáp án : A

Ví dụ 5: Giả sử có khai triển (1-2x)ⁿ = a₀+a₁x + a₂x²+....+a_nxⁿ. Tìm a₅ biết a₀+a₁+a₂ =71

A.672x⁵    B.-672     C.-672x⁵    D.672

Hướng dẫn giải :

Đáp án : B

Ví dụ 6: Trong khai triển (3x²+1/x)ⁿ hệ số của x³ là 3⁴.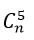 giá trị của n là:

A.15    B.12    C.9    D.18

Hướng dẫn giải :

Đáp án : C

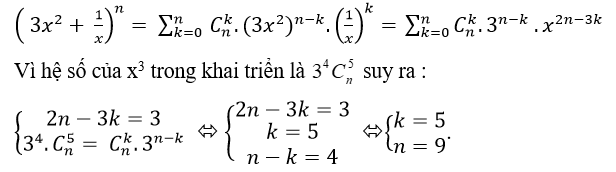
Vậy n = 9

Ví dụ 7: Hệ số của số hạng chứa x¹⁰ trong khai triển nhị thức (x+2)ⁿ biết n là số nguyên dương thỏa mãn

A.35    B.44    C.30    D.22

Hướng dẫn giải :

Đáp án : D

+ Theo công thức khai triển nhị thức Newton ta có:

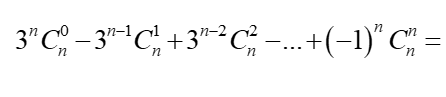
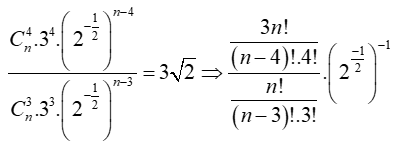
+ Theo giả thiết ta có: 2n = 2048 = 211 ⇔ n=11.

Như vậy ta có:

Suy ra hệ số của x¹⁰ ứng với k= 1 và đó là số: 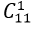.2=22

Ví dụ 8: Tìm số nguyên dương bé nhất n sao cho trong khai triển (1+ x)ⁿ có hai hệ số liên tiếp có tỉ số là 7/15.

A.20    B.21    C.22    D.23

Hướng dẫn giải :

Đáp án : B

C. Bài tập trắc nghiệm

Câu 1: Tìm số hạng không chứa x trong khai triển (1+x+1/x)ⁿ biết n >= 2 là số nguyên dương thỏa mãn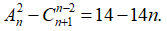

A.73789    B.73788    C.72864    D.56232

Lời giải:

Đáp án : A

Câu 2: Tìm hệ số chứa x¹⁰ trong khai triển P(x) = (1/4 x^2+x+1)².(x+2)³ⁿ với n là số tự nhiên thỏa mãn hệ thức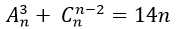

A.2956096    B.1876542     C.2768952    D.2987684

Lời giải:

Đáp án : A

Câu 3: Tìm hệ số của x⁴ trong khai triển P(x)= (1- x – 3x³)ⁿ với n là số tự nhiên thỏa mãn hệ thức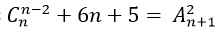

A.480    B.360    C.240     D.420

Lời giải:

Đáp án : A

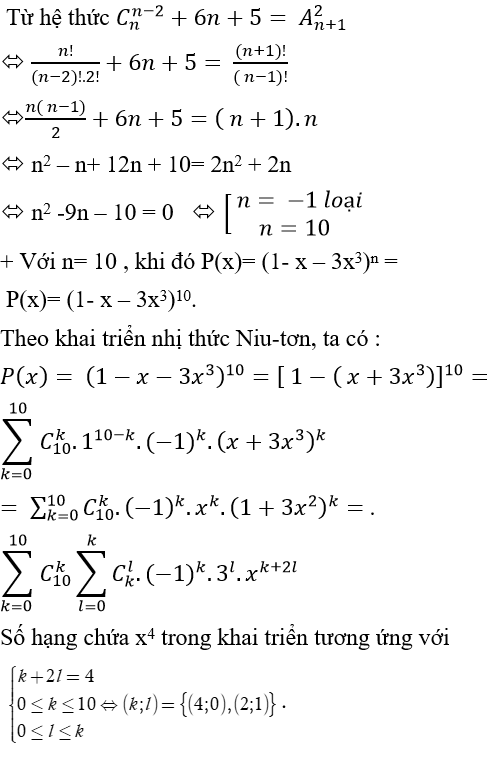
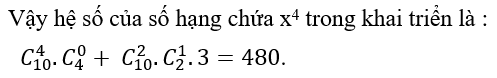
Câu 4: Số hạng thứ 3 trong khai triển (2x+1/x²)ⁿ không chứa x. Tìm x biết rằng số hạng này bằng số hạng thứ hai của khai triển (1+x³)³⁰.

A.-1    B.2    C.−1    D.-2

Lời giải:

Đáp án : B

Áp dụng nhị thức Niu- ton ta có:

Số hạng thứ ba tương ứng với k= 2. Do số hạng thứ ba không chứa x nên ta có:

n - k - 2k= 0 ⇔ n = 3k = 6 ( vì k = 2)

⇒ Hệ số không chứa x trong khai triển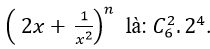

+ Mà số hạng thứ hai trong khai triển (1+ x³ )³⁰ là 30.x³

+ Từ giả thiết suy ra: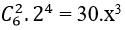

⇔ x³ = 8 ⇔ x= 2

Vậy x = 2.

Câu 5: Trong khai triển (1+x)ⁿ biết tổng các hệ số 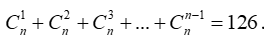. Hệ số của số hạng chứa x³ bằng:

A.15    B.21    C.35    D.20

Lời giải:

Đáp án : C

Ta có:

Cho x= 1 ta được:

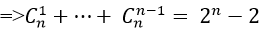
Theo giả thiết ta có: 2ⁿ – 2= 126 ⇔ 2ⁿ = 128 = 2⁷ nên n= 7

Hệ số cần tìm là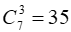

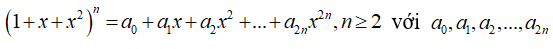
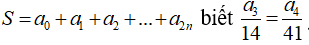
Câu 6: Cho khai triển: là các hệ số. Tính tổng .

A.S = 3¹⁰    B.S = 3¹²    C.S = 2¹⁰    D.S = 2¹²

Lời giải:

Đáp án : A

Theo giả thiết ta có:

Thay x = 1 ta được: S= a₀+ a₁ + a₂+ ..+ a_2n = P(1 )= 3ⁿ (*)

Ta xác định n:

Với 0≤q≤p≤n thì số hạng tổng quát khi khai triển tam thức

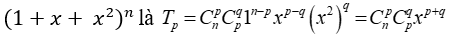
Hệ số của x3 ứng với:

Suy ra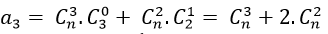

Hệ số của x4 ứng với: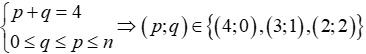

Suy ra:

Theo giả thiết ta có:

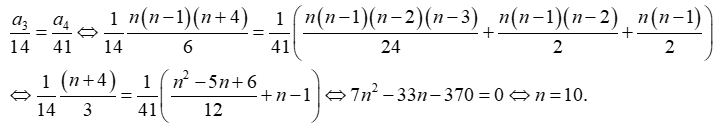
Thay vào (*) ta được: S= a₀+ a₁ + a₂+ ..+ a_2n =3¹⁰

Câu 7: Cho khai triển (1/√2+3)ⁿ. Tìm n biết tỉ số giữa số hạng thứ năm và thứ tư bằng 3√2.

A.8    B.10    C.6    D.7

Lời giải:

Đáp án : D

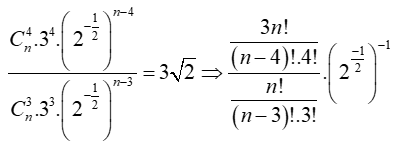
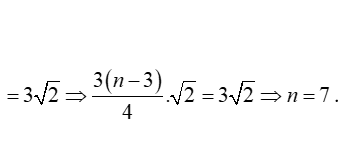
⇒ Vậy n = 7.