Cách tính chu kì tuần hoàn của hàm số lượng giác cực hay - Toán lớp 11

---

Cách tính chu kì tuần hoàn của hàm số lượng giác cực hay

Với Cách tính chu kì tuần hoàn của hàm số lượng giác cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính chu kì tuần hoàn của hàm số lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

+ Hàm số y= f(x) xác định trên tập hợp D được gọi là hàm số tuần hoàn nếu có số T ≠ 0 sao cho với mọi x ∈ D ta có x+T ∈ D;x-T ∈ D và f(x+T)=f(x).

Nếu có số T dương nhỏ nhất thỏa mãn các điều kiện trên thì hàm số đó được goi là một hàm số tuần hoàn với chu kì T.

+ Cách tìm chu kì của hàm số lượng giác ( nếu có ):

Hàm số y = k.sin(ax+b) có chu kì là T= 2π/|a|

Hàm số y= k.cos(ax+ b) có chu kì là T= 2π/|a|

Hàm số y= k.tan( ax+ b) có chu kì là T= π/|a|

Hàm số y= k.cot (ax+ b ) có chu kì là: T= π/|a|

Hàm số y= f(x) có chu kì T1; hàm số T2 có chu kì T2 thì chu kì của hàm số y= a.f(x)+ b.g(x) là T = bội chung nhỏ nhất của T1 và T2

B. Ví dụ minh họa

Ví dụ 1: Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. y= sin x

B. y = x+ 1

C. y=x² .

D. y=(x-1)/(x+2) .

Lời giải:

Chọn A

Tập xác định của hàm số: D= R

Với mọi x ∈ D , k ∈ Z ta có x-2kπ ∈ D và x+2kπ ∈ D , sin(x+2kπ)=sinx .

Vậy y=sinx là hàm số tuần hoàn.

Ví dụ 2: Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. y= sinx- x

B. y= cosx

C. y= x.sin x

D.y=(x²+1)/x

Lời giải:

Chọn B

Tập xác định của hàm số: D=R .

mọi x ∈ D , k ∈ Z ta có x-2kπ ∈ D và x+2kπ ∈ D,cos(x+2kπ)=cosx .

Vậy y= cosx là hàm số tuần hoàn.

Ví dụ 3: Chu kỳ của hàm số y= cosx là:

A. 2kπ

B. 2π/3

C. π

D. 2π

Lời giải:

Chọn D

Tập xác định của hàm số: D= R

Với mọi x ∈ D;k ∈ Z, ta có x-2kπ ∈ D và x+2kπ ∈ D thỏa mãn: cos⁡( x+k2π)=cosx

Vậy y= cosx là hàm số tuần hoàn với chu kì (ứng với k= 1) là số dương nhỏ nhất thỏa mãn cos⁡( x+k2π)=cosx

Ví dụ 4: Chu kỳ của hàm số y= tanx là:

A.2π

B.π/4

C.kπ,k ∈ Z

D.π

Lời giải:

Chọn D

Tập xác định của hàm số:D= R\{π/2+kπ,k ∈ Z }

Với mọi x ∈ D;k ∈ Z ta có x-kπ ∈ D;x+kπ ∈ D và tan (x+kπ)=tanx

Vậy là hàm số tuần hoàn với chu kì π (ứng với k= 1) là số dương nhỏ nhất thỏa mãn tan (x+kπ)=tanx

Ví dụ 5. Hàm số y= 2tan ( 2x-100) có chu kì là?

A. T= π/4

B. T= π/2

C. 2π

D. π

Lời giai

Hàm số y= k.tan( ax+ b) có chu kì là: T= π/|a|

Áp dụng: Hàm số y= 2tan( 2x - 100) có chu kì là: T= π/2

Chọn B.

Ví dụ 6. Hàm số y = - π.sin⁡( 4x-2998) là

A. T= π/2

B. T= π/4

C.2π

D. π

Lời giải:

Hàm số y= k.sin(ax+ b) có chu kì là: T= 2π/|a| .

Chu kì của hàm số: y = - π.sin⁡( 4x-2998) là: T= 2π/4= π/2

Chọn A

Ví dụ 7. Tìm chu kì của hàm số y= 10π cos⁡(π/2-20 x)?

A. 20 π

B. 10π

C. π/20

D. π/10

Lời giải

Hàm số y= k.cos(ax+ b) có chu kì là: T= 2π/|a| .

Chu kì của hàm số: y = 20 π.cos⁡(π/2-20 x) là: T= 2π/|-20| = π/10

Chọn D.

Ví dụ 8. Tìm chu kì của hàm số y= ( 1)/2π cot⁡(π/10+10 x)?

A. π

B. 10π

C. π/20

D. π/10

Lời giải

Hàm số y= k.cot(ax+ b) có chu kì là: T= π/|a| .

Chu kì của hàm số: y = ( 1)/2π cot⁡(π/10+10 x) là: T= π/|10| = π/10

Ví dụ 9. Tìm chu kì của hàm số y= 2sin2x+1

A. 1

B. 2π

C. π

D. 4π

Lời giải:

Ta có: y= 2sin2x+1 = 1- cos2x +1= 2- cos2x

⇒ Chu kì của hàm số đã cho là: T= 2π/2= π

Chọn C.

Ví dụ 10. Tìm chu kì của hàm số: y=sin⁡( 2x- π)+ 1/2 tan⁡( x+ π)

A. π

B. 2π

C. π/2

D. Đáp án khác

Lời giải

Hàm số y= f(x) = sin( 2x- π) có chu kì T₁= 2π/2= π.

Hàm số y= g(x)= 1/2 tan⁡( x+ π) có chu kì T₂= π/1= π

⇒ Chu kì của hàm số đã cho là: T= π.

Chọn A.

Ví dụ 11. Tìm chu kì của hàm số y= 1/2 tan⁡( x- π/2)+ 1/10 cot⁡( x/2- π)

A. π

B. 2π

C. π/2

D. Đáp án khác

Lời giải:

Ta có: chu kì của hàm số y= f(x)= 1/2 tan⁡( x- π/2) là T₁= π/1= π

Chu kì của hàm số y=g(x)= 1/10 cot⁡( x/2- π) là T₂= π/(1/2)= 2π

Suy ra chu kì của hàm số đã cho là: T=2π

Chọn B.

Ví dụ 12. Tìm chu kì của hàm số y= 〖sin〗^2 x+cos⁡( 2x+ π/3)

A.π/2

B. 2π

C. 4π

D. π

Lời giải:

Ta có: y= sin² x+cos⁡( 2x+ π/3)= (1-cos2x)/2+cos⁡( 2x+ π/3)

chu kì của hàm số y= f(x)= (1-cos2x)/2 là T₁= 2π/2= π

Chu kì của hàm số y= g(x)= cos⁡( 2x+ π/3) là T₂= 2π/2=π

⇒ chu kì của hàm số đã cho là: T= π

Chọn D

Ví dụ 13. Tìm chu kì của hàm số y= 2sin2x. sin4x

A.π/2

B. 2π

C. π

D. 4π

Lời giải:

Ta có: y= 2. sin2x. sin4x = cos 6x+ cos2x

Chu kì của hàm số y = cos6x là T₁= 2π/6= π/3

Chu kì của hàm số y= cos2x là T₂= 2π/2= π

⇒ chu kì của hàm số đã cho là: T= π

Chọn C

Ví dụ 14. Tìm chu kì của hàm số y= sin3x + cos2x

A. 2π

B. π

C. 4π

D. Đáp án khác

Lời giải:

Ta có y= sin3x + cos2x = 1/4 (3sinx-sin3x) + cos2x

Chu kì của hàm số y= 3/4 sinx là T₁= 2π

Chu kì của hàm số y =(- 1)/4 sin3x là T₂=2π/3

Chu kì của hàm số y= cos2 là T₃= 2π/2= π

⇒ Chu kì của hàm số đã cho là: T= 2π

Chọn A.

C. Bài tập vận dụng

Câu 1:Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. y= x. cosx

B.y= x. tanx

C. y= tanx

D.y=1/x .

Lời giải:

Chọn C

Xét hàm số y= tanx:

Tập xác định của hàm số: D=R\{π/2+kπ,k ∈ Z } .

Với mọi x ∈ D ,k ∈ Z ta có x-kπ ∈ D và x+kπ ∈ D ,tan(x+kπ)=tanx .

Vậy y= tanx là hàm số tuần hoàn.

Câu 2:Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A.y=sinx/x

B.y= tanx+ x

C.y=x²+1

D. y= cotx

Lời giải:

Chọn D

Xét hàm số y= cotx:

Tập xác định: D=R\{kπ,k ∈ Z } .

Với mọi x ∈ D ,k ∈ Z ta có x-kπ ∈ D và x+kπ ∈ D ,cot(x+kπ)=cotx

Vậy y= cot x là hàm tuần hoàn.

Câu 3:Chu kỳ của hàm số y= sinx là:

A.k2π,k ∈ Z

B.π/2

C.π

D.2π

Lời giải:

Chọn D

Tập xác định của hàm số:D=R\{kπ,k ∈ Z } .

Với mọi x ∈ D;k ∈ Z ta có x-k2π ∈ D và x+k2π ∈ D; sin⁡(x+k2π2)=sinx

Vậy y= sinx là hàm số tuần hoàn với chu kì 2π (ứng với k=1 ) là số dương nhỏ nhất thỏa mãn sin⁡(x+k2π2)=sinx.

Câu 4:Chu kỳ của hàm số y= cot x là:

A.2π

B.π/2

C.π

D.kπ,k ∈ Z .

Lời giải:

Chọn C

Tập xác định của hàm số: D=R\{kπ,k ∈ Z } .

Với mọi x ∈ D;k ∈ Z ta có x-kπ ∈ D và x+ kπ ∈ D; cot(x+kπ)=cotx .

Vậy y=cotx là hàm số tuần hoàn với chu kì π (ứng với k= 1) là số dương nhỏ nhất thỏa cot(x+kπ)=cotx.

Câu 5:Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. y= sinx

B. y= x+ sinx

C. y= x.cosx

D.y=sinx/x .

Lời giải:

Chọn A

Hàm số y= x+sinx không tuần hoàn. Thật vậy:

Tập xác định D=R.

Giả sử f(x+T)=f(x) với ∀ x ∈ D.

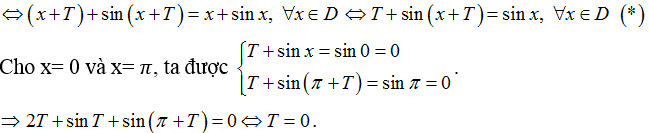
Điều này trái với định nghĩa là T > 0.

Vậy hàm số không phải là hàm số tuần hoàn.

+ Tương tự chứng minh cho các hàm số y= x.cosx và không tuần hoàn.

+ Hàm số y= sin x là hàm số tuần hoàn với chu kì T=2π

Câu 6:Tìm chu kì T của hàm số y= sin( π/10-5x).

A. T= 2π/5

B. T= 5π/2

C.T=π/2 .

D.C.T=π/8 .

Lời giải:

Chọn A

Hàm số y= k.sin(ax+b) tuần hoàn với chu kì .

Áp dụng: Hàm số y= sin( π/10-5x) tuần hoàn với chu kì T= 2π/|- 5| = 2π/5.

Câu 7:Tìm chu kì T của hàm số y=cos⁡( x/2+2198π).

A. T= 4π

B.T=2π

C. T= π/2

D.π .

Lời giải:

Chọn A

Hàm số y= cos(ax+ b) tuần hoàn với chu kì .

Áp dụng: Hàm số y=cos⁡( x/2+2198π) tuần hoàn với chu kì T= 2π/(1/2)=4π.

Câu 8:Tìm chu kì T của hàm số y= 1/3 cos⁡( 50πx-50 π).

A. T= 1/25

B. T= 50

C. T= 25

D. T= 1/50

Lời giải:

Chọn A

Hàm số y= 1/3 cos⁡( 50πx-50 π) tuần hoàn với chu kì T= 2π/(50 π)= 1/25.

Câu 9:Tìm chu kì T của hàm số y=3tan⁡(3π x+3π).

A.T=π/3 .

B.T=4/3 .

C.T=2π/3 .

D.T=1/3 .

Lời giải:

Chọn D

Hàm số y= k.tan( ax+ b) tuần hoàn với chu kì T= π/|a|

Áp dụng: Hàm số y=3 tan⁡( 3π x+3π) tuần hoàn với chu kì T= π/3π= 1/3

Câu 10:Tìm chu kì T của hàm số y= tan x+ cot 3x.

A. T= 4π

B. T= π

C. T= 3π

D.T= π/3 .

Lời giải:

Chọn B

Hàm số y= cot(ax+b) tuần hoàn với chu kì T= π/|a|.

Áp dụng: Hàm số y= cot3x tuần hoàn với chu kì T₁= π/3 .

Hàm số y= tanx tuần hoàn với chu kì T₂= π .

Suy ra hàm số y= tanx+cot3x tuần hoàn với chu kì T= π

Nhận xét: T là bội chung nhỏ nhất của T₁ và T₂ .

Câu 11:Tìm chu kì T của hàm số: y= cos⁡(2x/3+ π)+2cot⁡x

A. T= 4π

B. T= π

C. T= 3π

D.T= π/3 .

Lời giải:

Chọn C

Hàm số y= cos(2x/3+ π) tuần hoàn với chu kì T₁=2π/(2/3)=3π .

Hàm số y= 2cot x tuần hoàn với chu kì T₂= π.

Suy ra y= cos⁡(2x/3+ π)+2cot⁡x hàm số tuần hoàn với chu kì 3π .

Câu 12:Tìm chu kì T của hàm số y=sin(x/2)-tan(2x+π/4 ) .

A. T= 4π

B. T= π

C. T= 3π

D.T= π/3 .

Lời giải:

Chọn A

Hàm số y=sin(x/2) tuần hoàn với chu kì T₁=4π.

Hàm số y=-tan(2x+π/4 ) tuần hoàn với chu kì T₂= π/2 .

Suy ra hàm số y=sin(x/2)-tan(2x+π/4 ) tuần hoàn với chu kì T=4π.

Câu 13:Tìm chu kì T của hàm số y= 2cos2x + 4π.

A. T= 4π

B. T=2π

C. T= π

D. T= 2

Lời giải:

Chọn C

Ta có y= 2cos2x + 4π = cos2x + 1+ 4π.

Suy ra hàm số tuần hoàn với chu kì T= π.

Câu 14:Hàm số nào sau đây có chu kì khác π?

A.y=sin(-2x+π/3)

B.y=cos2(x+π/4)

C. y= tan(-2x+ 100).

D. y=cosx. sinx

Lời giải:

Chọn C

Ta xét các phương án:

+ Phương án A. Chu kì của hàm số là T= 2π/|- 2| = π

+ Phương án B. Chu kì của hàm số là T= 2π/|2| = π

+ Phương án C: Hàm số có chu kì T= π/|-2| = π/2 .

+ Phương án D. Ta có: y=cosx. sinx= 1/2.sin⁡2x

Hàm số có chu kì là: T= 2π/|2| = π

Vậy hàm số y = tan(- 2x+ 100) có chu kì khác π.

Câu 15:Hàm số nào sau đây có chu kì khác 2π?

A. y= cos³x

B.sin(x/2)cos(x/2) .

C. y= sin2(x+ 2)

D.cos²(x/2+1) .

Lời giải:

Chọn C

+ Hàm số y= cos³x=1/4(cos3x+3cosx)

Do y= cos 3x có chu kì T1 = 2π/3 và y= 3cosx có chu kì là T2 = 2π

⇒ hàm số y= cos³x có chu kì là 2π ( là bội chung nhỏ nhất của T₁ và T₂ ).

+Hàm số y=sin(x/2)cos(x/2)=1/2sinx có chu kì là T= 2π/1= 2π.

+ Hàm số y= sin2(x+ 2)=1/2-1/2cos(2x+4) có chu kì là T= 2π/2 = π

+ Hàm số y=cos²(x/2+1)= 1/2+1/2cos(x+2) có chu kì là T= 2π.

Câu 16:Hai hàm số nào sau đây có chu kì khác nhau?

A. y= 2cosx và y= cot(x/2) .

B. y= - 3sinx và y= tan2x

C. y= sin(x/2) và y= cos(x/2) .

D. y= 2tan (2x -10) và y= cot( 10- 2x)

Lời giải:

Chọn B

+ Hai hàm số y= 2cosx và y= cot(x/2) có cùng chu kì là 2π.

+ Hai hàm số y= - 3sinx có chu kì là 2π, hàm số y= tan2x có chu kì là π/2 .

+ Hai hàm số y= sin(x/2) và y= cos(x/2) có cùng chu kì là 4π.

+ Hai hàm số y= 2.tan(2x-10) và y= cot (10- 2x) có cùng chu kì là π/2 .