Vận dụng định nghĩa đạo hàm vào giải các bài toán thực tiễn lớp 11 (bài tập + lời giải)

---

Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Vận dụng định nghĩa đạo hàm vào giải các bài toán thực tiễn lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Vận dụng định nghĩa đạo hàm vào giải các bài toán thực tiễn.

Vận dụng định nghĩa đạo hàm vào giải các bài toán thực tiễn lớp 11 (bài tập + lời giải)

1. Phương pháp giải

Để giải quyết các bài toán thực tế bằng cách vận dụng định nghĩa đạo hàm ta thực hiện các bước sau:

Bước 1: Tìm hiểu bài toán thực tế, phân tích, xác định giả thuyết, các tham số, biến số, thiết lập mối quan hệ giữa các yếu tố.

Bước 2: Sử dụng công cụ tính đạo hàm theo định nghĩa và ý nghĩa của đạo hàm để giải quyết bài toán.

Bước 3: Kết luận.

2. Ví dụ minh họa

Ví dụ 1. Một vật chuyển động thẳng xác định bởi phương trình s(t) = 3t³ + 8t² + 2. Tính vận tốc tức thời của chuyển động tại t = 2, trong đó s tính bằng mét, thời gian t tính bằng giây.

Hướng dẫn giải:

Vận tốc tức thời của chuyển động tại t = 2 là:

v(2) = s'(2) = $\underset{\text{t}\to \text{2}}{\lim }\frac{3{\text{t}}^3+8{\text{t}}^2+2-\left(3\cdot 2^3+8\cdot 2^2+2\right)}{\text{t}-2}$

$=\underset{\text{t}\to \text{2}}{\lim }\frac{3{\text{t}}^3+8{\text{t}}^2-56}{\text{t}-2}=\underset{\text{t}\to \text{2}}{\lim }\left(3{\text{t}}^{\text{2}}+14\text{t}+28\right)=68$.

Vậy vận tốc tức thời của chuyển động tại t = 2 là 68 m/s.

Ví dụ 2. Một viên đạn được bắn lên trời từ một vị trí cách mặt đất 1 000 m theo phương thẳng đứng với vận tốc ban đầu là v₀ = 245 m/s (bỏ qua sức cản của không khí).

a) Tìm thời điểm t₀ mà tại đó viên đạn đạt độ cao lớn nhất và sẽ bắt đầu rơi. Khi đó viên đạn cách mặt đất bao nhiêu mét?

b) Sau bao nhiêu giây (kể từ lúc bắn), viên đạn rơi xuống đến mặt đất?

Hướng dẫn giải:

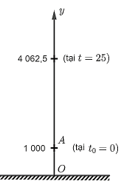
a) Chọn trục Oy theo phương thẳng đứng, chiều dương hướng từ mặt đất lên trời, gốc O ở mặt đất và A là vị trí viên đạt được bắn lên, gốc thời gian (tức lúc t = 0) được tính từ vị trí A như hình vẽ dưới.

Khi đó chuyển động của viên đạn là chuyển động biến đổi đều với vận tốc ban đầu là v₀ = 245 m/s và với gia tốc là g = – 9,8 m/s². (Gia tốc nhận giá trị âm vì vectơ gia tốc ngược chiều dương của trục Oy). Phương trình chuyển động của viên đạn là

y = 1 000 + 245t – 4,9t².

Ta tính được v(t) = y' = 245 – 9,8t.

Viên đạn đạt độ cao lớn nhất và sẽ bắt đầu rơi khi v(t) = 0, tức là 245 – 9,8t = 0.

Từ đó suy ra t = 25 (s).

Khi đó viên đạn cách mặt đất là y(25) = 1 000 + 245 ∙ 25 – 4,9 ∙ 25² = 4 062, 5 (m).

b) Viên đạn rơi đến đất khi y = 0. Vậy nếu gọi t₁ là thời gian kể từ khi viên đạn được bắn lên trời đến khi nó rơi tới đất thì t₁ phải là nghiệm dương của phương trình

0 = 1 000 + 245t – 4,9t², tức là t₁ ≈ 54 (s).

3. Bài tập tự luyện

Bài 1. Một vật rơi tự do với phương trình chuyển động $\text{s}=\frac{1}{2}{\text{gt}}^{\text{2}}$, trong đó g = 9,8 m/s² và t tính bằng giây. Vận tốc của vật tại thời điểm t = 7 là

A. 66,8 m/s;

B. 88,6 m/s;

C. 68,6 m/s;

D. 86,6 m/s.

Bài 2. Cho chuyển động thẳng xác định bởi phương trình s(t) = t³ – t² + 2t + 5, trong đó t tính bằng giây, và s tính bằng mét. Vận tốc của chuyển động tại thời điểm t = 3 là:

A. 23 m/s;

B. 32 m/s;

C. 23 cm/s;

D. 32 cm/s.

Bài 3. Chi phí sản xuất x mét vải là C(x) = 1200 + 12x – 0,1x². Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm một mét vải từ x mét vải lên x + 1 mét vải. Khi đó hàm chi phí biên C'(x) là:

A. 12 + 0,2x;

B. 0,2x – 12;

C. –12 – 0,2x;

D. 12 – 0,2x.

Bài 4. Cho biết điện lượng trong một dây dẫn theo thời gian biểu thị bởi hàm số Q = 5t + 3 (t tính bằng giây, Q tính bằng culông). Tính cường độ của dòng điện trong dây dẫn tại t = 8.

A. 4 A;

B. 5 A;

C. 6 A;

D. 8 A.

Bài 5. Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là 19,6 m/s thì độ cao h của nó (tính bằng mét) sau t giây được cho bởi công thức h = 19,6t – 4,9t². Vận tốc của vật khi nó chạm đất là

A. 9,6 m/s;

B. – 9,6 m/s;

C. – 19,6 m/s;

D. 19,6 m/s.

Bài 6. Cho chuyển động thẳng có phương trình $\text{s(t)}=\frac{1}{3}{\text{t}}^{\text{3}}-4{\text{t}}^2+20\text{t}-13$, trong đó s tính bằng centimét, t tính bằng giây. Vận tốc nhỏ nhất của chuyển động là:

A. 4 cm/s;

B. 3,5 cm/s;

C. 2 cm/s;

D. 1,8 cm/s.

Bài 7. Một chất điểm chuyển động thẳng theo phương trình $\text{s(t)}=\frac{1}{3}{\text{t}}^{\text{3}}-2{\text{t}}^2+6\text{t}+1$, trong đó s tính bằng centimét, t tính bằng giây. Vận tốc nhỏ nhất của chất điểm đạt được tại thời điểm t bằng bao nhiêu giây?

A. t = 1 giây;

B. t = 2 giây;

C. t = 6 giây;

D. t = 7 giây.

Bài 8. Một vật chuyển động thẳng theo phương trình s(t) = 4t² – t³, trong đó s tính bằng mét, t tính bằng giây. Vật có thể đạt vận tốc lớn nhất là bao nhiêu?

A. 8 m/s;

B.  m/s;

C.  m/s;

D. 4 m/s.

Bài 9. Một đoàn tàu chuyển động thẳng khởi hành từ một nhà ga. Quãng đường s(t) đi được của đoàn tàu là một hàm số của thời gian t (s), hàm số đó là s(t) = 6t² – t³. Vận tốc của tàu đạt giá trị lớn nhất tại thời điểm t bằng:

A. 1 giây;

B. 2 giây;

C. 6 giây;

D. 12 giây.

Bài 10. Sau khi phát hiện một bệnh dịch, các y bác sĩ ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f(t) = – t³ + 45t² – 22. Nếu f'(t₀) là tốc độ bệnh truyền nhiễm (người/ngày) tại thời điểm t₀. Hỏi tốc độ truyền bệnh sẽ lớn nhất vào ngày bao nhiêu?

A. 9;

B. 10;

C. 12;

D. 15.