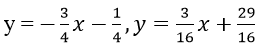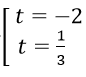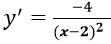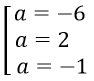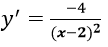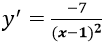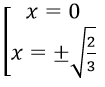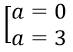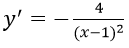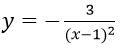Viết phương trình tiếp tuyến đi qua một điểm - Toán lớp 11

---

Viết phương trình tiếp tuyến đi qua một điểm

Với Viết phương trình tiếp tuyến đi qua một điểm Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình tiếp tuyến đi qua một điểm từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải & Ví dụ

Phương trình tiếp tuyến của đồ thị (C): y = f(x) đi qua điểm M(x₁; y₁)

Cách 1 :

- Phương trình đường thẳng (d) đi qua điểm M có hệ số góc là k có dạng :

y = k( x – x₁) + y₁.

- (d) tiếp xúc với đồ thị (C) tại N(x₀; y₀) khi hệ:

có nghiệm x_o

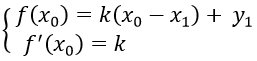
Cách 2 :

- Gọi N(x₀; y₀) là tọa độ tiếp điểm của đồ thị (C) và tiếp tuyến (d) qua điểm M, nên (d) cũng có dạng y = y’₀(x – x₀) + y₀.

- (d) đi qua điểm nên có phương trình : y₁ = y₀'(x₁ – x₀) + y₀     (*)

- Từ phương trình (*) ta tìm được tọa độ điểm N(x₀; y₀) , từ đây ta tìm được phương trình đường thẳng (d)

Ví dụ minh họa

Bài 1: Cho hàm số y = 2x³ - 3x² + 5 có đồ thị là (C). Tìm phương trình các đường thẳng đi qua điểm A (19/12; 4) và tiếp xúc với đồ thị (C) của hàm số.

Hướng dẫn:

Hàm số đã cho xác định D = R

Ta có: y’ = 6x² – 6x

Gọi M(x₀; y₀)∈(C)⇔ y₀ = 2x₀³ - 3x₀² + 5 và y'(x₀) = 6x₀² - 6x₀

Phương trình tiếp tuyến Δ của (C) tại M có dạng:

      y – y₀ = y’(x₀)(x – x₀)

⇔ y - 2x₀³ + 3x₀² - 5 = (6x₀² - 6x₀)(x - x₀ )

⇔ (6x₀²- 6x₀)x - 4x₀³ + 3x₀³ + 5 = y

A ∈ Δ ⇔4 =(6x₀² - 6x₀).(19/12) - 4x₀³ + 3x₀³ + 5

⇔8x₀³ - 25x₀² + 19x₀ - 2 = 0

⇔x₀ = 1 hoặc x₀ = 2 hoặc x₀ = 1/8

Với x₀ = 1 ⇒ Δ:y = 4

Với x₀ = 2 ⇒ Δ:y = 12x - 15

Với x₀ = 1/8 ⇒ Δ:y = (-21/32)x + 645/128

Bài 2: Cho hàm số: 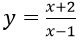có đồ thị là (C) và điểm A(0; m). Xác định m để từ A kẻ được 2 tiếp tuyến đến (C) sao cho hai tiếp điểm tương ứng nằm về hai phía đối với trục Ox.

Hướng dẫn:

TXĐ: D = R\{1}

Gọi điểm M(x₀; y₀).

Ta có y’ = -3/(x-1)²

Tiếp tuyến Δ tại M của (C) có phương trình:

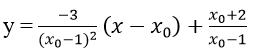
Vì tiếp tuyến qua A(0; m) nên ta có:

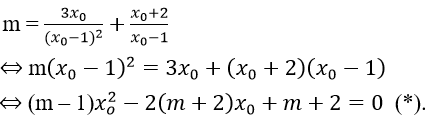
Yêu cầu bài toán ⇔ (*) có hai nghiệm a, b khác 1 sao cho

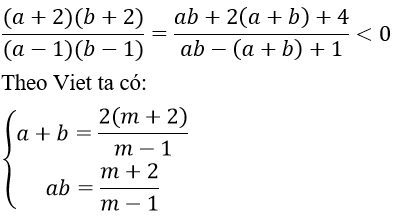
Khi đó:

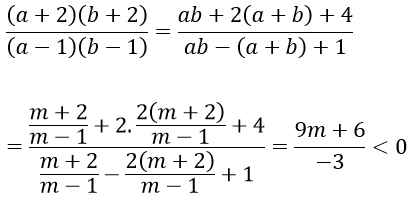
Ta có: (*) có hai nghiệm a, b khác 1 sao cho

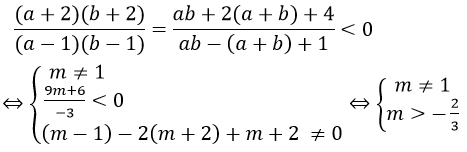
Vậy 1 ≠ m > (-2/3) là những giá trị cần tìm

Bài 3: Cho hàm số y = x³ – 2x² + (m – 1)x + 2m có đồ thị là (Cm). Tìm m để từ điểm M(1; 2) vẽ đến (Cm) đúng hai tiếp tuyến.

Hướng dẫn:

Ta có: y' = 3x² - 4x + m-1. Gọi A(a; b) là tọa độ tiếp điểm.

Phương trình tiếp tuyến Δ tại A:

y =(3a²-4a+m-1)(x-a) + a³-2x²+(m-1)a+2m

Vì M ∈ Δ ⇔2 = (3a²-4a+m-1)(1-a) + a³-2x²+(m-1)a+2m

⇔2a³+5a²-4a+3m-3 = 0      (*)

Yêu cầu bài toán tương đương với (*) có đúng hai nghiệm phân biệt. (1)

Xét hàm số: h(t) = 2t³+5t²-4t,   t∈R.

Ta có: h’(t) = 6t²+10t-4. Cho h’(t) = 0 ⇒

Bảng biến thiên

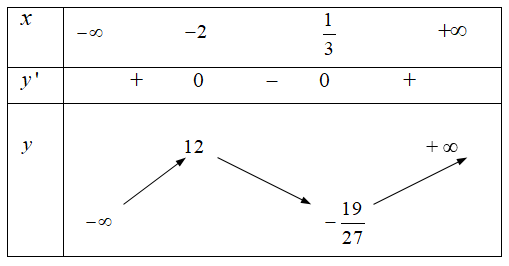
Dựa vào bảng biến thiên, suy ra (1)

⇒ là những giá trị cần tìm.

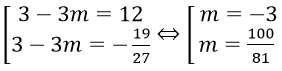
Bài 4: Cho hàm số y = (1/3)x³-2x²+3x có đồ thị là (C). Tìm phương trình các đường thẳng đi qua điểm A(4/9; 4/3) và tiếp xúc với đồ thị (C) của hàm số.

Hướng dẫn:

Ta có: y' = x²-4x+3. Gọi A(a; b) là tọa độ tiếp điểm.

Phương trình tiếp tuyến Δ tại A:

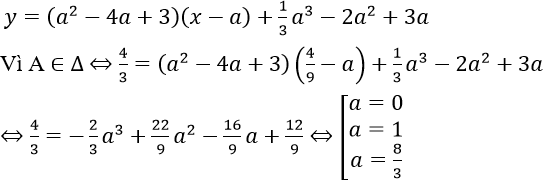
Với a = 0, phương trình tiếp tuyến cần tìm là: y = 3x

Với a = 1, phương trình tiếp tuyến cần tìm là: y = 4/3

Với a = 8/3, phương trình tiếp tuyến cần tìm là: y = (-5/9)x + 128/81

Bài 5: Viết phương trình tiếp tuyến của đồ thị hàm số 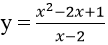, biết tiếp tuyến đi qua điểm M(6;4)

Hướng dẫn:

Ta có:

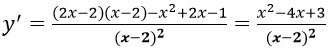
Gọi A(a; b) là tọa độ tiếp điểm

Phương trình tiếp tuyến Δ tại A:

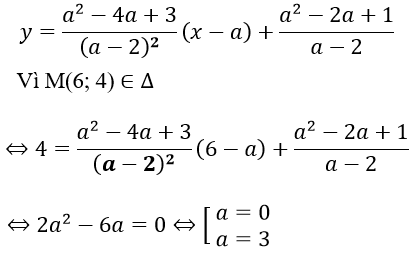
Với a = 0, phương trình tiếp tuyến cần tìm là: y = (3/4)x - 1/2

Với a = 3, phương trình tiếp tuyến cần tìm là: y = 4

Bài 6: Viết phương trình tiếp tuyến d với đồ thị (C): 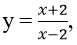biết d đi qua điểm A(-6; 5)

Hướng dẫn:

Ta có:

Gọi A(a; b) là tọa độ tiếp điểm.

Phương trình tiếp tuyến Δ tại A:

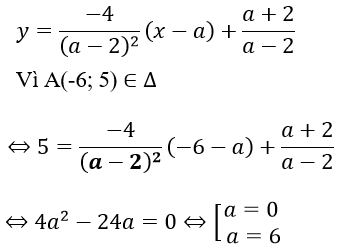
Với a = 0, phương trình tiếp tuyến cần tìm là: y = -x-1

Với a = 6, phương trình tiếp tuyến cần tìm là: y = (-1/4)(x-6) + 2 = (-1/4)x + 7/2

Bài 7: Viết phương trình tiếp tuyến của (C): y = x³ – 2x² + x + 4 đi qua điểm M( -4; -24)

Hướng dẫn:

Ta có: y' = 3x²-4x+1. Gọi A(a; b) là tọa độ tiếp điểm

Phương trình tiếp tuyến Δ tại A:

y = (3a²-4a+1)(x-a)+a³-2a²+a+4

Vì A(-4; -24) ∈ Δ ⇔ -24 = (3a²-4a+1)(-4-a)+a³-2a²+a+4

⇔ -2a³-10a²+16a+24 = 0 ⇔

Với a = -6, phương trình tiếp tuyến cần tìm là: y = 133(x+6)-240 = 133x+508

Với a = 2, phương trình tiếp tuyến cần tìm là: y = 5(x-2)+6 = 5x-10

Với a = -1, phương trình tiếp tuyến cần tìm là: y = 8(x+1)+2 = 8x+10

B. Bài tập vận dụng

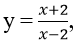
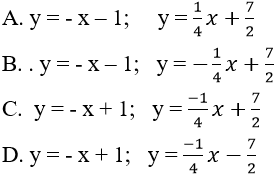
Bài 1: Cho hàm số tiếp tuyến của đồ thị hàm số kẻ từ điểm (-6; 5) là

Lời giải:

Đáp án: B

Chọn B

Ta có:

Gọi A(a; b) là tọa độ tiếp điểm

Phương trình tiếp tuyến Δ tại A:

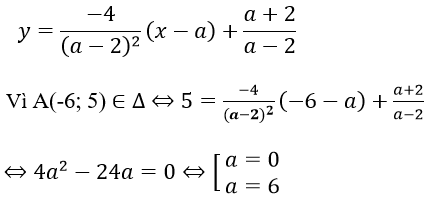
Với a = 0, phương trình tiếp tuyến cần tìm là: y = -x-1

Với a = 6, phương trình tiếp tuyến cần tìm là: y = (-1/4)(x-6)+2 = (-1/4)x + 7/2

Bài 2: Tiếp tuyến kẻ từ điểm (2; 3) tới đồ thị hàm số 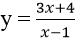là:

A. y = -28x + 59; y = x + 1

B. y = -24x + 51; y = x + 1

C. y = -28x + 59

D. y = - 28x + 59; y = -24x + 51

Lời giải:

Đáp án: C

Chọn C

Ta có:

Gọi A(a; b) là tọa độ tiếp điểm.

Phương trình tiếp tuyến Δ tại A:

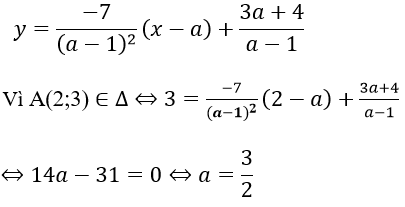
Với a = 3/2, phương trình tiếp tuyến cần tìm là: y = -28(x-3/2) + 17 = -28x + 59

Bài 3: Cho hàm số 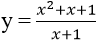có đồ thị (C). Phương trình tiếp tuyến của (C) đi qua điểm A(- 1; 0) là:

A.y = (3/4)x

B. y = (3/4)(x+1)

C. y = 3(x + 1)

D. y = 3x + 1

Lời giải:

Đáp án: B

Chọn B.

Ta có:

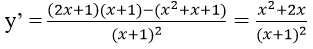
Gọi d là phương trình tiếp tuyến của (C) có hệ số góc k

Vì A(-1; 0) ∈ d suy ra d: y = k(x + 1) = kx + k

d tiếp xúc với (C) khi hệ 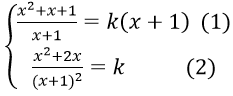có nghiệm

Thay (2) vào (1) ta được x = 1, suy ra k = y’(1) = 3/4

Vậy phương trình tiếp tuyến của (C) đi qua điểm A(-1; 0) là: y = (3/4)(x+1)

Bài 4: Qua điểm A(0; 2) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x⁴ - 2x² + 2

A. 2                B. 3                C. 0                D. 1

Lời giải:

Đáp án: B

Chọn B.

Gọi d là tiếp tuyến của đồ thị hàm số đã cho.

Vì A(0; 2) ∈ d nên phương trình của d có dạng: y = kx + 2

Vì d tiếp xúc với đồ thị (C) nên hệ 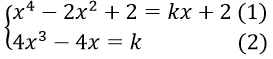có nghiệm

Thay (2) và (1) ta suy ra được :

Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)

Bài 5: Cho hàm số y = - x⁴ + 2x² có đồ thị (C). Xét hai mệnh đề:

(I) Đường thẳng Δ: y = 1 là tiếp tuyến với (C) tại M(-1; 1) và tại N(1; 1)

(II) Trục hoành là tiếp tuyến với (C) tại gốc toạ độ

Mệnh đề nào đúng?

A. Chỉ (I)

B. Chỉ (II)

C. Cả hai đều sai

D. Cả hai đều đúng

Lời giải:

Đáp án: D

Chọn đáp án D

Ta có y’(-1) = y’(1) = 0 ⇒ (I) đúng

Ta có y’(0) = 0 ⇒ (II) đúng

Bài 6: Cho hàm số y = x³ – 6x² + 9x – 1 có đồ thị là (C). Từ một điểm bất kì trên đường thẳng x = 2 kẻ được bao nhiêu tiếp tuyến đến (C):

A. 2                B. 1                C. 3                D. 0

Lời giải:

Đáp án: B

Chọn đáp án B.

Xét đường thẳng kẻ từ một điểm bất kì trên đường thẳng x = 2 có dạng d: y = k(x – 2)

d là tiếp tuyến của (C)

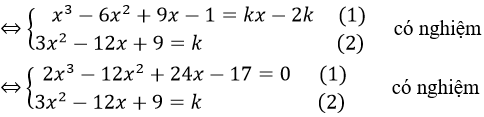
Phương trình bậc ba có duy nhất một nghiệm tương ứng cho ta một giá trị k. Vậy có một tiếp tuyến.

Bài 7: Đường thẳng y = 3x + m là tiếp tuyến của đồ thị hàm số y = x³ + 2 khi m bằng

A. 1 hoặc -1

B. 4 hoặc 0

C. 2 hoặc -2

D.3 hoặc -3

Lời giải:

Đáp án: B

Chọn B.

Đường thẳng y = 3x + m và đồ thị hàm số y = x³ + 2 tiếp xúc nhau

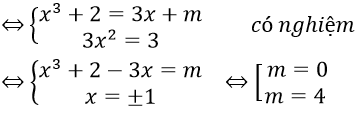
Bài 8: Định m để đồ thị hàm số y = x³ – mx² + 1 tiếp xúc với đường thẳng d: y = 5?

A. m = -3                B. m = 3                C. m = -1                D. m = 2

Lời giải:

Đáp án: A

Chọn A

Đường thẳng y = 5 và đồ thị hàm số y = x³ – mx² + 1 tiếp xúc nhau

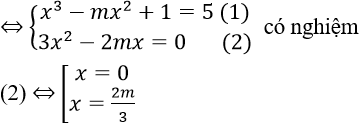
+ Với x = 0 thay vào (1) không thỏa mãn

+ Với x = 2m/3 thay vào (1) ta có: m³ = -27⇔ m = -3

Bài 9: Phương trình tiếp tuyến của (C): y = x³ biết nó đi qua điểm M(2; 0) là:

A. y = 27x ± 54

B. y = 27x – 9; y = 27x – 2

C. y = 27x ± 27

D. y = 0; y = 27x – 54

Lời giải:

Đáp án: D

Chọn D.

+ y’ = 3x²

+ Gọi A(a ; b) là tiếp điểm. Phương trình tiếp tuyến của (C) tại A là:

y = 3a²(x – a) + a³    (d)

+ Vì tiếp tuyến (d) đí qua M(2 ; 0) nên ta có phương trình:

0 = 3a²(2 – a) + a³ ⇔

+ Với a = 0 thay vào (d) ta có tiếp tuyến y = 0

+ Với a = 3 thay vào (d) ta có tiếp tuyến y = 27x – 54

Bài 10: Cho hàm số y = x² – 5x – 8 có đồ thị (C). Khi đường thẳng y = 3x + m tiếp xúc với (C) thì tiếp điểm sẽ có tọa độ là:

A. M(4; 12)             B. M(- 4; 12)             C. M(-4; - 12)             D. M( 4; - 12)

Lời giải:

Đáp án: D

Đáp án D

Đường thẳng d: y = 3x + m tiếp xúc với (C) ⇒ d là tiếp tuyến với (C) tại A(a; b)

y’ = 2x – 5

y’(a) = 3 ⇒ a = 4, b = -12

Bài 11: Cho hàm số 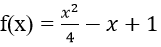có đồ thị (C). Từ điểm M(2; -1) có thể kẻ đến (C) hai tiếp tuyến phân biệt. Hai tiếp tuyến này có phương trình:

A. y = -x + 1 và y = x – 3

B. y = 2x – 5 và y = -2x + 3

C. y = -x – 1 và y = - x + 3

D. y = x + 1 và y = - x – 3

Lời giải:

Đáp án: A

Chọn A

Gọi N(a;b) là tiếp điểm

y’ = x/2 - 1

Phương trình tiếp tuyến tại N là:

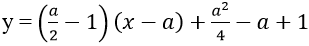
Mà tiếp tuyến đi qua M(2; -1)

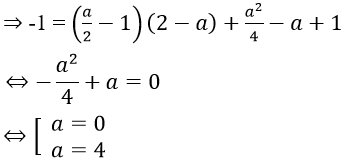
Với a = 0, phương trình tiếp tuyến là : y = -x + 1

Với a = 4. Phương trình tiếp tuyến : y = x – 3

Bài 12: Cho hàm số y = x³ + 3x² – 6x + 1 (C). Tìm phương trình tiếp tuyến của đồ thị (C) trong các phương trình sau, biết tiếp tuyến đi qua điểm N(0; 1).

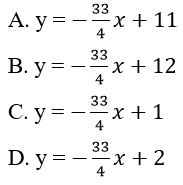
Lời giải:

Đáp án: C

Chọn C

Gọi M(a; b) là tiếp điểm

Ta có: y’ = 3x² + 6x – 6

Phương trình tiếp tuyến có dạng:

y = (3a²+6a-6)(x-a)+a³+3a²-6a+1

Vì tiếp tuyến đi qua N(0; 1) nên ta có:

1 = (3a²+6a-6)(0-a)+a³+3a²-6a+1

⇔ 2a³+3a² = 0

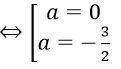
a = 0. Phương trình tiếp tuyến: y = -6x + 1

a = -3/2. Phương trình tiếp tuyến: y = (-33/4)x + 1

Bài 13: Cho hàm số y = x⁴ + x² + 1 (C). Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đi qua điểm M(-1; 3).

A. y = -6x – 2

B. y = -6x – 9

C. y = -6x – 3

D. y = -6x – 8

Lời giải:

Đáp án: C

Chọn C

Ta có: y’ = 4x³ + 2x. Gọi M(a; b) là tiếp điểm

Phương trình tiếp tuyến có dạng:

y = (4a³+2a)(x-a)+a⁴+a²+1

Vì tiếp tuyến đi qua M(-1; 3) nên ta có:

3 = (4a³+2a)(-1-a)+a⁴+a²+1

⇔3a⁴+4a³+a²+2a+2 = 0

⇔(a+1)²(3a²-2a+2) = 0

⇔ a = -1

Phương trình tiếp tuyến: y = -6x – 3

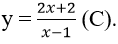
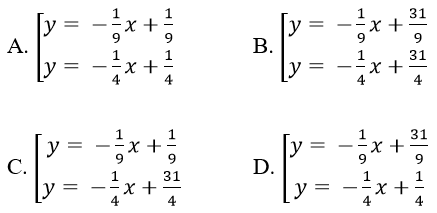
Bài 14: Cho hàm số Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua điểm A(4; 3)

Lời giải:

Đáp án: D

Chọn D

Hàm số xác định với mọi x ≠ 1. Ta có:

Gọi M(a; b) là tiếp điểm, suy ra phương trình tiếp tuyến của (C):

Vì tiếp tuyến đi qua A(4; 3) nên ta có:

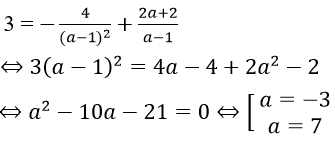
+ a = 7. Phương trình tiếp tuyến y = (-1/9)x + 31/9

+ a = - 3. Phương trình tiếp tuyến y = (-1/4)x - 1/4

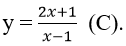
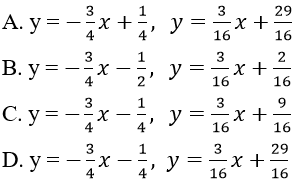
Bài 15: Cho hàm số Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đi qua A( - 7; 5).

Lời giải:

Đáp án: D

Chọn D

Ta có

Gọi M(a; b) là tiếp điểm. Do tiếp tuyến đi qua A(-7; 5) nên ta có:

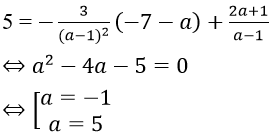
Từ đó ta tìm được các tiếp tuyến là: