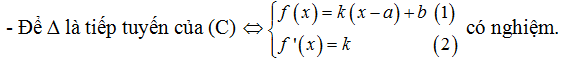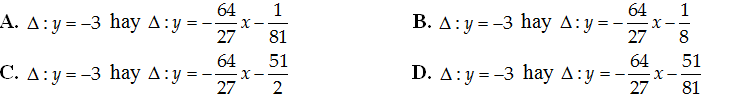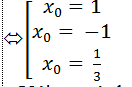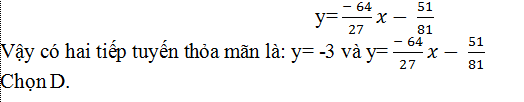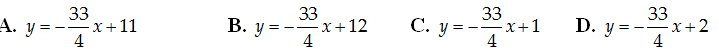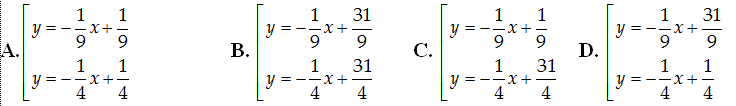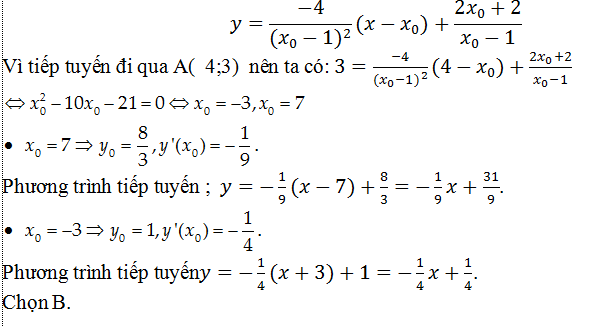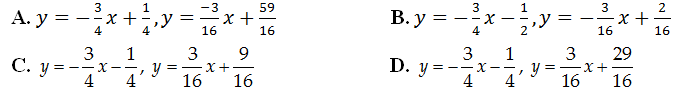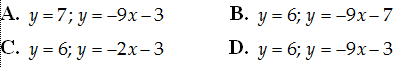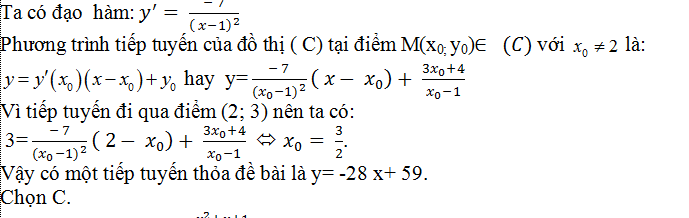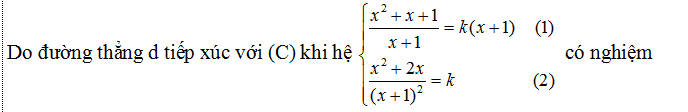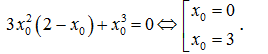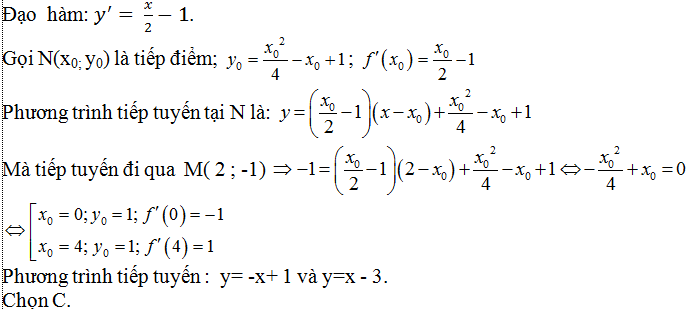Viết phương trình tiếp tuyến của đồ thị hàm số đi qua 1 điểm - Toán lớp 11

---

Viết phương trình tiếp tuyến của đồ thị hàm số đi qua 1 điểm

Với Viết phương trình tiếp tuyến của đồ thị hàm số đi qua 1 điểm Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình tiếp tuyến của đồ thị hàm số đi qua 1 điểm từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

*Ý nghĩa hình học của đạo hàm:

Đạo hàm của hàm số y= f(x) tại điểm x₀ là hệ số góc của tiếp tuyến với đồ thị (C) của hàm số tại điểm M₀(x₀; f(x₀) ).

Khi đó phương trình tiếp tuyến của (C) tại điểm M₀ là:

y–y₀=f' (x₀).(x–x₀)

A. Phương pháp giải

Cho (C) là đồ thị của hàm số y= f(x) và điểm A( a ; b).Viết phương trình tiếp tuyến với (C) biết tiếp tuyến đi qua A.

- Gọi ∆ là đường thẳng qua A và có hệ số góc k.

Khi đó tiếp tuyến ∆ có dạng : y= k(x- a)+ b (*)

- Thay (2) vào (1) ta có phương trình ẩn x. Tìm x thay vào (2) tìm k thay vào (*) ta có phương trình tiếp tuyến cần tìm.

B. Ví dụ minh họa

Ví dụ 1 : Cho hàm số y=2x⁴-4x²-1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua A( 1; -3).

Hướng dẫn giải

Ta có y'=8x³-8x

Gọi M(x₀; 2x₀⁴- 4x₀²-1) là một điểm thuộc đồ thị hàm số (C).

Tiếp tuyến ∆ tại M có phương trình:

y=(8x₀³-8x₀)(x-x₀)+2x₀⁴-4x₀²-1 ( *)

Vì tiếp tuyến ∆ đi qua A( 1; -3)nên ta có

+ Với x₀ = 1 thay vào (*) ta được phương trình tiếp tuyến: y= -3.

+ Với x₀= -1 thay vào (*) ta được phương trình tiếp tuyến: y= -3.

+ Với x₀= 1/3 thay vào (*) ta được phương trình tiếp tuyến:

Ví dụ 2. Cho ( C) là đồ thị của hàm số: y= x³+ 3x² – 6x+ 1. Viết phương trình tiếp tuyến của ( C) đi qua điểm N( 0; 1) .

Hướng dẫn giải

Gọi M( x₀; y₀ ) là tiếp điểm

Ta có đạo hàm của hàm số đã cho là: y'= 3x²+6x-6

Phương trình tiếp tuyến có dạng:

Vì tiếp tuyến đi qua N( 0;1) nên ta có:

1=(3x₀²+6x₀-6)(-x₀)+x₀³+3x₀²-6x₀+1

⇔2x₀³+3x₀²=0 ⇔x₀=0,x₀=-3/2

+ Nếu x⁰= 0 ⇒ y’(x⁰)= - 6.

⇒ Phương trình tiếp tuyến: y= -6x+ 1.

+ Nếu x₀=-3/2 thì y' (x₀ )= (- 33)/4; y₀= 107/8

⇒ Phương trình tiếp tuyến: y'=-33/4(x+3/2)+107/8=-33/4 x+1

Chọn C.

Ví dụ 3 Viết phương trình tiếp tuyến của đồ thị hàm số: y=x⁴+x²+1 biết tiếp tuyến đi qua điểm M( -1; 3).

A. y= -6x - 2       B. y= -6x- 9       C. y= -6x- 3       D. y= - 6x- 4

Hướng dẫn giải

Ta có đạo hàm : y’= 4³ + 2x. Gọi M( x₀; y₀) là tiếp điểm.

Phương trình tiếp tuyến có dạng:

y=(4x₀³+2x₀)(x-x₀)+x₀⁴+x₀²+1

Vì tiếp tuyến đi qua M( -1; 3) nên ta có:

⇔(x₀+1)² (3x₀²-2x₀+2)=0

⇔x₀=-1 ⇒y₀=3,y'(x₀)=-6

Phương trình tiếp tuyến: y – 3= - 6( x+ 1) hay y= - 6x – 3

Chọn C.

Ví dụ 4. Cho hàm số y=2x+2/x-1 (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua điểm A( 4; 3)

Hướng dẫn giải

Hàm số xác định với mọi

.

Ta có đạo hàm

Gọi M( x⁰; y⁰) là tiếp điểm, suy ra phương trình tiếp tuyến của (C):

Ví dụ 5. Tìm trên (C) : y= 2x³- 3x² + 1 những điểm M sao cho tiếp tuyến của (C) tại M cắt trục tung tại điểm có tung độ bằng 8.

A. M( 1; 0)       B. M(- 2; - 27)       C. M( -1; - 4)        D. M( 2; 5)

Hướng dẫn giải

Giả sử M(x₀;y₀)∈(C) ⇔ y₀=2x₀³-3x₀²+1.

Ta có đạo hàm: y'=6x²-6x.

Phương trình tiếp tuyến ⇔ tại M: y=(6x₀²-6x₀)(x-x₀)+2x₀³-3x₀²+1.

Gọi giao điểm của tiếp tuyến ∆ và trục tung là P ⇒ P( 0; 8)

⇔ đi qua P( 0; 8) nên thay tọa độ điểm M vào phương trình∆ ta được

8=-4x₀³+3x₀²+1 ⇔ x₀=-1.

Vậy M(-1; - 4)

Chọn C.

Ví dụ 6: Cho hàm số (C): y = (x+2)/(x-2) . Viết phương trình tiếp tuyến đi qua A(-6;5) của đồ thị (C).

A: y=x+1        B: y=-x-1        C: y=-x+1        D: Đáp án khác

Hướng dẫn giải

Ví dụ 7.Cho hàm số y=(2x+1)/(x-1) (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đi qua A( -7; 5).

Hướng dẫn giải

C. Bài tập vận dụng

Câu 1: Cho hàm số y=x³-3x²-9x+1có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua điểm A( -1; 6) .

Lời giải:

Ta có: y'=3(x²-2x-3). Gọi M(x₀; y₀) là tiếp điểm.

Phương trình tiếp tuyến ∆ tại M là:

y=3(x₀²-2x₀-3).( x- x₀ )+ x₀³-3x₀²-9x₀+1 ( *)

Do tiếp tuyến đi qua A nên ta có phương trình

6=3(x₀²-2x₀-3)(-1-x₀)+x₀³-3x₀²-9x₀+1

⇔x₀³-3x₀-2=0⇔(x₀+1)² (x₀-2)=0

⇔x₀=-1,x₀=2

+ Với x₀= -1thay vào (*) ta có phương trình tiếp tuyến là: y= 6

+ Với x₀= 2 thay vào (*) ta có phương trình tiếp tuyến là y= -9x - 3

Chọn D.

Câu 2: Tiếp tuyến kẻ từ điểm (2; 3) tới đồ thị (C) của hàm số y = (3x+4)/(x-1) là

A. y= -28x+ 59; y= x+ 1.        B. y= -24x + 51; y= x+ 1.

C. y= -28x + 59.        D. y= -28 x+ 59; y= -24 x+ 51

Lời giải:

Câu 3: Cho hàm số y= (x²+x+1)/(x+1) có đồ thị (C). Phương trình tiếp tuyến của (C) đi qua điểm

A( -1;0) là:

A. y= 3/4 x       B. y= 3/4 ( x+1)       C. y= 3( x+ 1)       D. y= 3x+1

Lời giải:

Gọi d là phương trình tiếp tuyến của (C) có hệ số góc k.

Vì A( -1;0) ∈d suy ra đường thẳng d có dạng: y= k( x+ 1)

Thay (2) vào (1) ta được x= 1 ⇒ k= y' (1)= 3/4.

Vậy phương trình tiếp tuyến của (C) đi qua điểm A( -1; 0) là: y= 3/4( x+1)

Chọn B.

Câu 4: Qua điểm A( 0; 2) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị (C) của hàm số

y= x⁴- 2x²+ 2

A. 2       B. 3       C.0       D. 1

Lời giải:

Gọi d là tiếp tuyến của đồ thị hàm số đã cho.

Đường thẳng d đi qua A(0; 2) và có hệ số góc k nên phương trình của d có dạng: y= kx+ 2

Câu 5: Phương trình tiếp tuyến của (C): y= x³ biết nó đi qua điểm M( 2; 0) là:

A. y= 27 x+ 54 và y= 27x- 54.       B. y= 27 x- 9 và y= 27 x - 2.

C. y= 27 x+ 27 và y= 27 x- 27.       D. y= 0 và y= 27x - 54.

Lời giải:

+ Đạo hàm y’= 3x²

+ Gọi A( x⁰ ; y⁰) là tiếp điểm. Phương trình tiếp tuyến của (C) tại A là:

+ Với x⁰= 0 thay vào (d) ta có tiếp tuyến y= 0.

+ Với x⁰ = 3 thay vào (d) ta có tiếp tuyến y= 27x- 54.

Chọn D

Câu 6: Cho hàm số f(x) =x²/4-x+1 , có đồ thị (C). Từ điểm M( 2; -1) có thể kẻ đến (C) hai tiếp tuyến phân biệt. Hai tiếp tuyến này có phương trình:

A. y= -x+ 1và y= x+ 3.        B. y= 2x- 5 và y= -2x + 3.

C. y= -x +1 và y = x - 3.        D.y= x+ 1và y= -x- 3.

Lời giải:

Câu 7: Cho đồ thị (C) của hàm số y= x²+ 2x+ 3. Viết phương trình tiếp tuyến d của đồ thị hàm số biết đường thẳng d đi qua điểm A( 1 ; 6).

A. y= 2x- 3        B. y= 3x+ 3        C.y= 4x+ 2        D. y= -x+ 7

Lời giải:

+ Đạo hàm : y’= 2x+ 2

+ Gọi M(x₀;x₀²+2x₀+3) là điểm thuộc đồ thị (C)

⇒ Phương trình tiếp tuyến tại M là :

y=( 2x₀+2)(x- x₀ )+ x₀²+2x₀+3 ( *)

+ Do tiếp tuyến d đi qua điểm A( 1 ; 6) nên ta có :

6= ( 2x₀+2)(1- x₀ )+ x₀²+2x₀+3

⇔ 2x₀-2x₀²+2-2x₀+ x₀²+2x₀+3=6

⇔ -x₀²+2x₀-1= 0 ⇔ x₀= 1

Thay vào (*) ta được phương trình tiếp tuyến cần tìm là ;

y= 4x+ 2

chọn C.