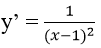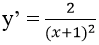60 bài tập trắc nghiệm Viết phương trình tiếp tuyến có đáp án - Toán lớp 11

---

60 bài tập trắc nghiệm Viết phương trình tiếp tuyến có đáp án

Với 60 bài tập trắc nghiệm Viết phương trình tiếp tuyến có đáp án Toán lớp 11 tổng hợp 60 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình tiếp tuyến từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

Bài 1: Cho đồ thị (H): 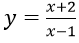và điểm A ∈ (H) có tung độ y = 4. Hãy lập phương trình tiếp tuyến của (H) tại điểm A.

A. y = x – 2

B. y = -3x – 11

C. y = 3x + 11

D. y = -3x + 10

Lời giải:

Đáp án: D

Chọn đáp án D.

Tập xác định: D = R\{1}

Đạo hàm: y’ = (-3)/(x-1)²

Tung độ của tiếp điểm là y = 4 nên 4 = [(x+2)/(x-1)] ⇔ x = 2

Tại M(2; 4), phương trình tiếp tuyến là y = -3x + 10

Bài 2: Tiếp tuyến của đồ thị hàm số 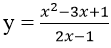tại giao điểm của đồ thị hàm số với trục tung có phương trình là:

A. y = x – 1

B. y = x + 1

C. y = x

D. y = -x

Lời giải:

Đáp án: A

Chọn A

Ta có:

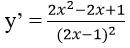
Giao điểm M của đồ thị với trục tung : x = 0 ⇒ y = -1

Hệ số góc của tiếp tuyến tại M là : k = y’(0) = 1

Phương trình tiếp tuyến tại điểm M là : y = x – 1

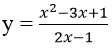
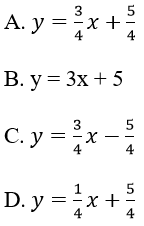
Bài 3: Cho đường cong (C): và điểm A ∈ (C) có hoành độ x = 3. Lập phương trình tiếp tuyến của (C) tại điểm A.

Lời giải:

Đáp án: A

Chọn A

Ta có:

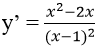
Tại điểm A ∈ (C) có hoành độ: x = 3 ⇒ y = 7/2

Hệ số góc của tiếp tuyến tại A là : k = y’(3) = 3/4

Phương trình tiếp tuyến tại điểm A là : y = (3/4)x + 5/4

Bài 4: Tiếp tuyến của đồ thị hàm số y = 1/√(2x) tại điểm A(1/2; 1) có phương trình là:

A. 2x + 2y = -3

B. 2x – 2y = -1

C. 2x + 2y = 3

D. 2x – 2y = 1

Lời giải:

Đáp án: C

Chọn C

Ta có:

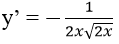
Hệ số góc của tiếp tuyến tại A là : k = y'(1/2) = -1

Phương trình tiếp tuyến tại điểm A là : 2x + 2y = 3

Bài 5: Tiếp tuyến của đồ thị hàm số f(x) = x³-2x²-2 tại điểm có hoành độ x = -2 có phương trình là:

A. y = 4x – 8.

B. y = 20x + 22.

C. y = 20x – 22.

D. y = 20x – 16.

Lời giải:

Đáp án: B

Chọn B.

Ta có: f'(x) = 3x² - 4x. Tại điểm A có hoành độ

x₀ = -2 ⇒ y₀ = f(x₀) = -18

Hệ số góc của tiếp tuyến tại A là : k = f'(-2) = 20

Phương trình tiếp tuyến tại điểm A là :

y = k(x-x₀) + y₀ ⇔ y = 20x + 22

Bài 6: Cho hàm số y = x³-3x+1 (C). Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với trục Oy.

A. y = 2, y = -1

B. y = 3, y = -1

C. y = 3, y = -2

D. x = 3, x = -1

Lời giải:

Đáp án: B

Chọn B.

Ta có: y’= 3x² - 3. Gọi M(x₀; y₀) là tiếp điểm

Vì tiếp tuyến vuông góc với Oy nên ta có: y’(x₀) = 0

Hay x₀ = ±1. Từ đó ta tìm được hai tiếp tuyến: y = 3, y = -1

Bài 7: Viết phương trình tiếp tuyến của đồ thị hàm số: y = 2x⁴-4x²+1 biết tiếp tuyến song song với đường thẳng y = 48x – 1

A. y = 48x – 9

B. y = 48x – 7

C. y = 48x – 10

D. y = 48x – 79

Lời giải:

Đáp án: D

Chọn D.

Ta có: y’ = 8x³ – 8x

Gọi M(x₀; y₀) là tiếp điểm.

Vì tiếp tuyến song song với đường thẳng y = 48x - 1

Nên ta có: y'(x₀) = 48 ⇔ x₀³ - x₀ - 6 = 0 ⇔ x₀ = 2

Suy ra y₀ = 17. Phương trình tiếp tuyến là:

y = 48(x – 2) + 17 = 48x - 79

Bài 8: Cho hàm số y = x⁴+x²+1    (C). Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến song song với đường thng y = 6x – 1

A. y = 6x – 2

B. y = 6x – 7

C. y = 6x – 8

D. y = 6x – 3

Lời giải:

Đáp án: D

Chọn D.

Ta có: y’ = 4x³ + 2x. Gọi M(x₀; y₀) là tiếp điểm

Vì tiếp tuyến song song với đường thẳng y = 6x - 1 nên ta có: y'(x₀) = 6 ⇔ 4x₀³ + 2x₀ - 6 = 0 ⇔ x₀ = 1 ⇒ y₀ = 3

Phương trình tiếp tuyến: y = 6x - 3

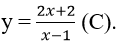
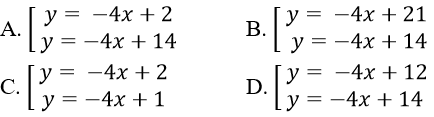
Bài 9: Cho hàm số Viết phương trình tiếp tuyến của (C), biết tiếp tuyến song song với đường thẳng d: y = -4x + 1.

Lời giải:

Đáp án: A

Chọn A

Hàm số xác định với mọi x ≠ 1. Ta có

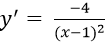
Gọi M(x₀; y₀) là tiếp điểm, suy ra phương trình tiếp tuyến của (C):

Vì tiếp tuyến song với đường thẳng d = - 4x + 1 nên ta có:

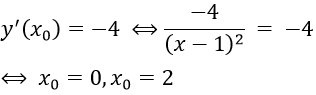
+ x₀ = 0 ⇒ y₀ = 2 ⇒ Δ: y = -4x + 2

+ x₀ = 2 ⇒ y₀ = 6 ⇒ Δ: y = -4x + 14

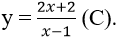
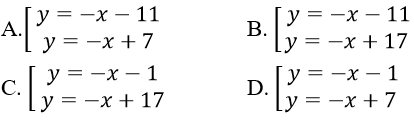
Bài 10: Cho hàm số Viết phương trình tiếp tuyến của (C), biết biết tiếp tuyến tạo với hai trục tọa độ một tam giác vuông cân.

Lời giải:

Đáp án: A

Chọn A

Hàm số xác định với mọi x ≠ 1. Ta có:

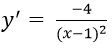
Gọi M(x₀; y₀) là tiếp điểm, suy ra phương trình tiếp tuyến của (C):

Vì tiếp tuyến tạo với hai trục tọa độ một tam giác vuông cân nên tiếp tuyến phải vuông góc với một trong hai đường phân giác y = ±x, do đó hệ số góc của tiếp tuyến bằng ±1 hay y' = ±1. Mà y' < 0, ∀x ≠ 1 nên ta có:

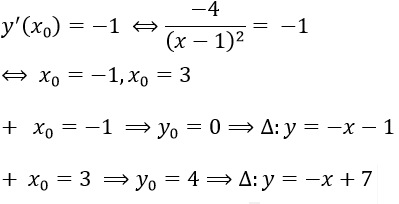
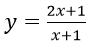
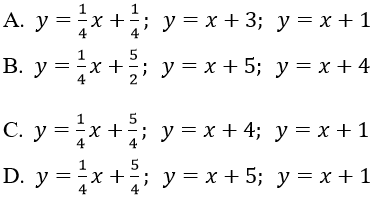
Bài 11: Viết phương trình tiếp tuyến d của đồ thị (C): biết d cách đều 2 điểm A(2;4) và B(-4; -2)

Lời giải:

Đáp án: D

Chọn D

Gọi M(x₀; y₀(x₀)), x₀ ≠ 1, là tọa độ tiếp điểm của d và (C)

Khi đó d có hệ số góc y’(x₀) = 1/(x₀+1)² và có phương trình là :

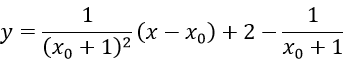
Vì d cách đều A, B nên d đi qua trung điểm I(-1;1) của AB hoặc cùng phương với AB.

TH1: d đi qua trung điểm I(-1;1), thì ta luôn có:

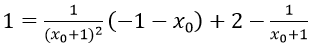
phương trình này có nghiệm x_o = 1

Với x₀ = 1 ta có phương trình tiếp tuyến d: y = (1/4)x + 5/4

TH2: d cùng phương với AB, tức là d và AB có cùng hệ số góc, khi đó

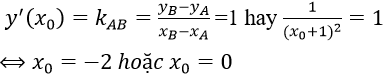
Với x₀ = -2 ta có phương trình tiếp tuyến d: y = x + 5

Với x₀ = 0 ta có phương trình tiếp tuyến d: y = x + 1

Vậy, có 3 tiếp tuyến thỏa mãn đề bài: y = (1/4)x + 5/4, y = x + 5, y = x + 1

Bài 12: Tìm m ∈ R để từ điểm M(1; 2) kẻ được 2 tiếp tuyến đến đồ thị (Cm): y = x³-2x²+(m-1)x+2m.

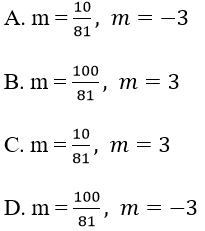
Lời giải:

Đáp án: D

Chọn D

Gọi N(x₀; y₀) ∈ (C). Phương trình tiếp tuyến (d) của A tại N là:

y = (3x₀²-4x₀+m-1)(x-x₀)+x₀³-2x₀²+(m-1)x₀+2m

M ∈ (d)⇔ 2x₀³ + 5x₀² - 4x₀ = 3-3m    (*)

Dễ thấy (*) là phương trình hoành độ giao điểm của đồ thị y = 3 – 3m và f(x₀) = 2x₀³ + 5x₀² - 4x₀

Xét hàm số f(x₀) = 2x₀³ + 5x₀²-4x₀ có f’(x₀) = 6x₀² + 10x₀-4

f’(x₀) = 0 ⇔ x₀ = -2 hoặc x₀ = 1/3

Lập bảng biến thiên, suy ra m = 100/81, m = -3

Bài 13: Cho hàm số y = 2x⁴-4x²-1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua A(1; -3).

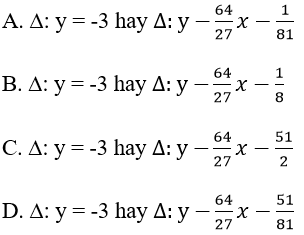
Lời giải:

Đáp án: D

Chọn D

Ta có y’ = 8x³ – 8x

Gọi M(x₀; y₀). Tiếp tuyến Δ tại M có phương trình:

y = (8x₀³-8x₀)(x-x₀) + 2x₀⁴-4x₀²-1

Vì tiếp tuyến Δ đi qua A(1;-3) nên ta có

-3 = (8x₀³-8x₀)(1-x₀ )+ 2x₀⁴-4x₀²-1

⇔ 3x₀⁴-4x₀³-2x₀²+4x₀-1 = 0 ⇔ (x₀-1)²(x₀+1)(3x₀-1) = 0

x₀ = ±1 ⇒ Δ: y = -3

x₀ = 1/3 ⇒ Δ: y = (-64/27)x - 51/81

Bài 14: Cho hàm số y = 2x⁴-4x²-1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến tiếp xúc với (C) tại hai điểm phân biệt.

A. Δ: y = -3            B. Δ: y = 4            C. Δ: y = 3            D. Δ: y = -4

Lời giải:

Đáp án: A

Chọn A

Ta có y’ = 8x³ – 8x

Gọi M(x₀; y₀). Tiếp tuyến Δ tại M có phương trình:

y = (8x₀³ - 8x₀)(x-x₀)+ 2x₀⁴-4x₀²-1. Giả sử Δ tiếp xúc với (C) tại điểm thứ hai N(n; 2n⁴-4n²-1)

Suy ra Δ: y = (8n³ – 8n)(x-n) + 2n⁴ – 4n² - 1

Nên ta có:

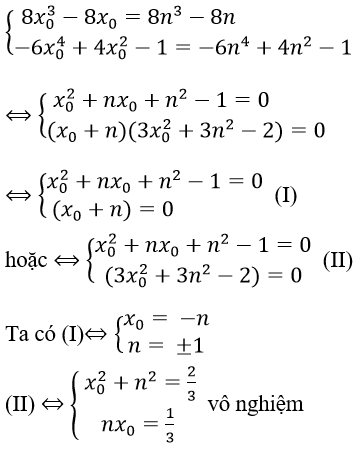
Vậy Δ: y = -3

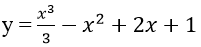
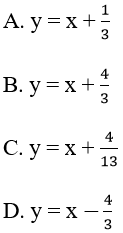
Bài 15: Cho (C) là đồ thị của hàm số . Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại A, B sao cho tam giác OAB vuông cân (O là gốc tọa độ ).

Lời giải:

Đáp án: B

Chọn B

Vì tam giác OAB là tam giác vuông tại O nên nó chỉ có thể vuông cân tại O, khi đó góc giữa tiếp tuyến (D) và trục Ox là 45°,suy ra hệ số góc của (D) là k_D = ±1

Trường hợp k_D = 1,khi đó phương trình (D) : y = x + a. (a ≠ 0)

(D) tiếp xúc (C) ⇔ 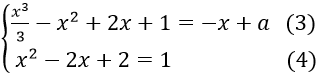có nghiệm.

(4)⇔ x²-2x+1 = 0 ⇒ x = 1

Thay x = 1 vaò phương trình (3) ta được a = 4/3

Vậy trong trường hợp này,phương trình (D): y = x + 4/3

Trường hợp k_D = -1, khi đó phương trình (D): y = - x + a

(D) tiếp xúc với (C) ⇔ 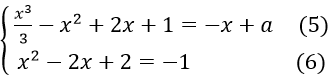có nghiệm.

(6)⇔ x²-2x+3 = 0. Phương trình này vô nghiệm nên hệ (5), (6) vô nghiệm,suy ra (D) : y = - x + a không tiếp xúc với (C)

Vậy phương trình tiếp tuyến cần tìm là y = x + 4/3.

Bài 16: Cho hàm số y = f(x), có đồ thị (C) và điểm Mo(x_o; f(x_o)) ∈ (C). Phương trình tiếp tuyến của (C) tại M_o là:

A. y = f '(x)(x-x_o)+y_o

B. y = f ' (x_o)(x-x_o)

C. y - y_o = f ' (x_o)(x-x_o)

D. y - y_o = f ' (x_o)x

Lời giải:

Đáp án: C

Chọn C

Bài 17: Hệ số góc của tiếp tuyến của đồ thị hàm số 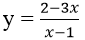tại giao điểm của đồ thị hàm số với trục hoành bằng :

A. 9            B. 1/9            C. -9            D. -1/9

Lời giải:

Đáp án: A

Chọn A

Tập xác định:D = R\{1}

Đạo hàm:

Đồ thị hàm số cắt trục hoành tại A(2/3; 0)

Hệ số góc của tiếp tuyến là y’(2/3) = 9

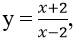
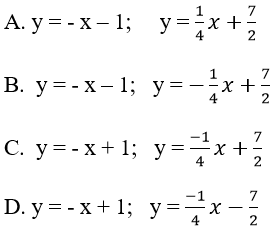
Bài 18: Cho hàm số tiếp tuyến của đồ thị hàm số kẻ từ điểm (-6; 5) là

Lời giải:

Đáp án: B

Chọn B.

Ta có: y' = (-4)/(x-2)². Gọi A(a; b) là tọa độ tiếp điểm.

Phương trình tiếp tuyến Δ tại A:

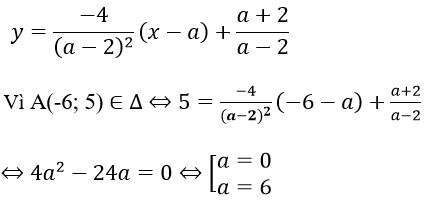
Với a = 0, phương trình tiếp tuyến cần tìm là: y = -x-1

Với a = 6, phương trình tiếp tuyến cần tìm là: y = (-1/4)(x-6)+2 = (-1/4)x + 7/2

Bài 19: Phương trình tiếp tuyến của đồ thị hàm số y = (x + 1)²(x – 2) tại điểm có hoành độ x = 2 là

A. y = - 8x + 4

B. y = 9x + 18

C. y = -4x + 4

D. y = 9x – 18

Lời giải:

Đáp án: D

Chọn D.

Gọi M(x_o; y_o) là tọa độ tiếp điểm.

Ta có x_o = 2 ⇒ y_o = 0

y = (x + 1)²(x – 2) = x³ – 3x – 3 nên y’ = 3x² – 3

Từ đó suy ra y’(2) = 9.

Vậy phương trình tiếp tuyến cần tìm là y = 9(x – 2) = 9x – 18

Bài 20: Hệ số góc của tiếp tuyến của đồ thị hàm số 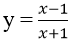tại giao điểm với trục tung bằng :

A. -2            B. 2            C. 1            D. -1

Lời giải:

Đáp án: B

Chọn B

Tập xác định: D = R\{-1}

Đạo hàm:

Đồ thị hàm số cắt trục tung tại điểm có x_o = 0 ⇒ y’(0) = 2

Bài 21: Tiếp tuyến kẻ từ điểm (2; 3) tới đồ thị hàm số 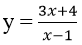là:

A. y = -28x + 59; y = x + 1

B. y = -24x + 51; y = x + 1

C. y = -28x + 59

D. y = - 28x + 59; y = -24x + 51

Lời giải:

Đáp án: C

Chọn C

Ta có:

Gọi A(a; b) là tọa độ tiếp điểm

Phương trình tiếp tuyến Δ tại A:

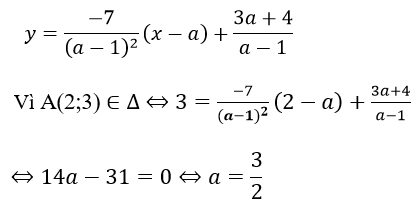
Với a = 3/2, phương trình tiếp tuyến cần tìm là: y = -28(x - 3/2) + 17 = -28x + 59

Bài 22: Phương trình tiếp tuyến của đồ thị của hàm số y = x(3 – x)² tại điểm có hoành độ x = 2 là

A. y = -3x + 8

B. y = -3x + 6

C. y = 3x – 8

D. y = 3x – 6

Lời giải:

Đáp án: A

Chọn A

Gọi M(x_o ; y_o) là tọa độ tiếp điểm

Ta có x_o = 2 ⇒ y_o = 2

y = (3 – x)²x = x³ – 6x² + 9x nên y’ = 3x² – 12x + 9

Từ đó suy ra y’(2) = - 3

Vậy phương trình tiếp tuyến cần tìm là y = -3(x – 2) + 2 = -3x + 8

Bài 23: Cho hàm số y = x³ – 3x² có đồ thị (C) có bao nhiêu tiếp tuyến của (C) song song đường thẳng y = 9x + 10

A. 1               B. 3               C. 2               D. 4

Lời giải:

Đáp án: C

Chọn C

Tập xác định: D = R

Đạo hàm: y’ = 3x² – 6x.k = 9 ⇒ 3x_o²-6x_o = 9 ⇔

Vậy có 2 tiếp tuyến thỏa mãn yêu cầu bài toán.

Bài 24: Cho hàm số 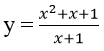có đồ thị (C). Phương trình tiếp tuyến của (C) đi qua điểm A(- 1; 0) là:

A. y = (3/4)x            B. y = (3/4)(x+1)            C. y = 3(x + 1)            D. y = 3x + 1

Lời giải:

Đáp án: B

Chọn B

Ta có:

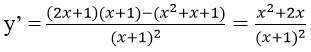
Gọi d là phương trình tiếp tuyến của (C) có hệ số góc k

Vì A(-1; 0) ∈ d suy ra d: y = k(x + 1) = kx + k

d tiếp xúc với (C) khi hệ 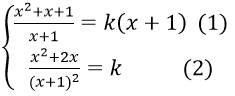có nghiệm

Thay (2) vào (1) ta được x = 1, suy ra k = y’(1) = 3/4

Vậy phương trình tiếp tuyến của (C) đi qua điểm A(-1; 0) là: y = (3/4)(x+1)

Bài 25: Cho đường cong (C): y = x². Phương trình tiếp tuyến của (C) tại điểm M( -1; 1) là

A. y = -2x + 1

B. y = 2x + 1

C. y = -2x - 1

D. y = 2x – 1

Lời giải:

Đáp án: C

Chọn C

Ta có y = x² nên y’ = 2x

Từ đó suy ra y’(-1) = -2

Vậy phương trình tiếp tuyết cần tìm là : y = -2(x + 1) +1 = -2x – 1

Bài 26: Gọi (C) là đồ thị của hàm số y = x⁴ + x. Tiếp tuyến của (C) vuông góc với đường thẳng d: x + 5y = 0 có phương trình là:

A. y = 5x – 3

B. y = 3x – 5

C. y = 2x – 3

D. y = x + 4

Lời giải:

Đáp án: A

Chọn A

Ta có : y’ = 4x³ + 1

Vì tiếp tuyến vuông góc với đường thẳng y = (-1/5)x nên tiếp tuyến có hệ số góc là 5

Khi đó ta có :

4x³ + 1 = 5 ⇔ x = 1 ⇒ y = 2

Phương trình tiếp tuyến của đồ thị hàm số tại M(1; 2) có dạng

y = 5(x – 1) + 2 = 5x – 3

Bài 27: Qua điểm A(0; 2) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x⁴ - 2x² + 2

A. 2            B. 3            C. 0            D. 1

Lời giải:

Đáp án: B

Chọn B.

Gọi d là tiếp tuyến của đồ thị hàm số đã cho.

Vì A(0; 2) ∈ d nên phương trình của d có dạng: y = kx + 2

Vì d tiếp xúc với đồ thị (C) nên hệ 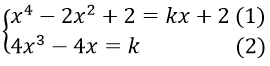có nghiệm

Thay (2) và (1) ta suy ra được

Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)

Bài 28: Cho hàm số 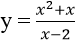. Phương trình tiếp tuyến tại A(1; -2) là

A. y = -4( x – 1) – 2

B. y = -5( x – 1) + 2

C. y = -5( x – 1) – 2

D. y = -3(x – 1) – 2

Lời giải:

Đáp án: C

Chọn C

Ta có

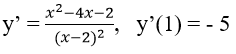
Phương trình tiếp tuyến cần tìm: y = -5(x – 1) – 2 = -5x + 3

Bài 29: Gọi (C) là đồ thị hàm số 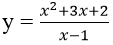. Tìm tọa độ các điểm trên (C) mà tiếp tuyến tại đó với (C) vuông góc với đường thẳng có phương trình y = x + 4

A. (1 + √3; 5+3√3),(1-√3; 5 -3√3)

B. (2; 12)

C. (0; 0)

D. (-2; 0)

Lời giải:

Đáp án: A

Chọn A.

Tập xác định: D = R\{1}

Đạo hàm:

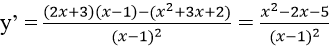
Giả sử a là hoành độ điểm thỏa mãn yêu cầu bài toán ⇒ y’(a) = -1

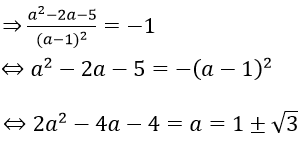
Bài 30: Cho hàm số y = - x⁴ + 2x² có đồ thị (C). Xét hai mệnh đề:

(I) Đường thẳng Δ: y = 1 là tiếp tuyến với (C) tại M(-1; 1) và tại N(1; 1)

(II) Trục hoành là tiếp tuyến với (C) tại gốc toạ độ

Mệnh đề nào đúng?

A. Chỉ (I)

B. Chỉ (II)

C. Cả hai đều sai

D. Cả hai đều đúng

Lời giải:

Đáp án: D

Chọn đáp án D

Ta có y’(-1) = y’(1) = 0 ⇒ (I) đúng

Ta có y’(0) = 0 ⇒ (II) đúng

Bài 31: Cho hàm số 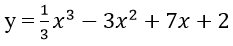. Phương trình tiếp tuyến tại A(0;2) là:

A. y = 7x + 2

B. y = 7x - 2

C. y = - 7x + 2

D. y = - 7x - 2

Lời giải:

Đáp án: A

Chọn A.

Ta có : y’ = x² – 6x + 7

Hệ số góc tiếp tuyến y’(0) = 7

Phương trình tiếp tuyến tại A(0 ; 2): y = 7x + 2

Bài 32: Biết tiếp tuyến (d) của hàm số y = x³ – 2x + 2 vuông góc với đường phân giác góc phần tư thứ nhất. Phương trình (d) là:

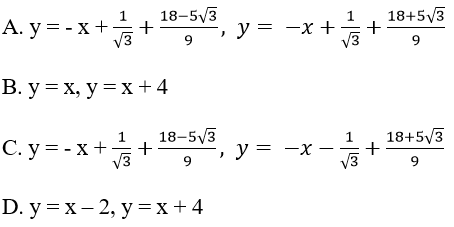
Lời giải:

Đáp án: C

Chọn C.

Tập xác định: D = R

y’ = 3x² – 2

Đường phân giác góc phần tư thứ nhất có phương trình Δ: x = y

⇒ (d) có hệ số góc là – 1

3x² – 2 = -1 ⇔ x = ± 1/√3

Phương trình tiếp tuyến cần tìm là

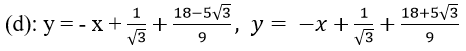
Bài 33: Cho hàm số y = x³ – 6x² + 9x – 1 có đồ thị là (C). Từ một điểm bất kì trên đường thẳng x = 2 kẻ được bao nhiêu tiếp tuyến đến (C):

A. 2               B. 1               C. 3               D. 0

Lời giải:

Đáp án: B

Chọn đáp án B

Xét đường thẳng kẻ từ một điểm bất kì trên đường thẳng x = 2 có dạng d: y = k(x – 2)

d là tiếp tuyến của (C) ⇔

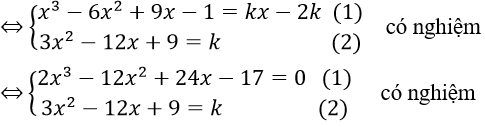
Phương trình bậc ba có duy nhất một nghiệm tương ứng cho ta một giá trị k. Vậy có một tiếp tuyến

Bài 34: Gọi (P) là đồ thị của hàm số y = 2x² – x + 3. Phương trình tiếp tuyến với (P) tại điểm mà (P) cắt trục tung là:

A. y = -x + 3

B. y = -x - 3

C. y = 4x – 1

D. y = 11x + 3

Lời giải:

Đáp án: A

Chọn A

Ta có : (P) cắt trục tung tại điểm M(0; 3)

y’ = 4x – 1

Hệ số góc tiếp tuyến : y’(0) = - 1

Phương trình tiếp tuyến của đồ thị (P) tại M(0; 3) là y = -x + 3

Bài 35: Tìm hệ số góc của tiếp tuyến với đồ thị y = tanx tại điểm có hoành độ x = π/4.

A. k = 1               B. k = 0.5               C. k = √2/2               D. 2

Lời giải:

Đáp án: D

Chọn D

y = tanx ⇒ y’ = 1/(cos²x)

Hệ số góc của tiếp tuyến với đồ thị y = tanx tại điểm có hoành độ x = π/4 là k = y’(π/4) = 2

Bài 36: Đường thẳng y = 3x + m là tiếp tuyến của đồ thị hàm số y = x³ + 2 khi m bằng

A. 1 hoặc -1

B. 4 hoặc 0

C. 2 hoặc -2

D. 3 hoặc -3

Lời giải:

Đáp án: B

Chọn B

Đường thẳng y = 3x + m và đồ thị hàm số y = x³ + 2 tiếp xúc nhau

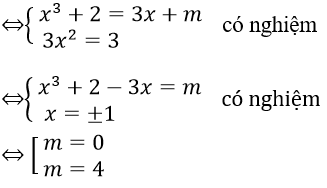
Bài 37: Đồ thị (C) của hàm số 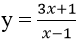cắt trục tung tại điểm A. Tiếp tuyến của (C) tại điểm A có phương trình là:

A. y = - 4x – 1

B. y = 4x – 1

C. y = 5x – 1

D. y = - 5x – 1

Lời giải:

Đáp án: A

Chọn A

Ta có : điểm A(0 ; -1)

y’ = (-4)/(x-1)² ⇒ hệ số góc của tiếp tuyến y’(0) = -4

Phương trình tiếp tuyến của đồ thị (C) tại điểm A(0 ; -1) là :

y = -4x – 1

Bài 38: Hệ số góc của tiếp tuyến của đường cong 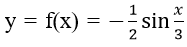tại điểm có hoành độ x_o = π là:

A. -√3/12               B. √3/12               C. -1/12               D. 1/12

Lời giải:

Đáp án: C

Chọn C

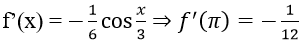
Bài 39: Định m để đồ thị hàm số y = x³ – mx² + 1 tiếp xúc với đường thẳng d: y = 5?

A. m = -3               B. m = 3               C. m = -1               D. m = 2

Lời giải:

Đáp án: A

Chọn A.

Đường thẳng y = 5 và đồ thị hàm số y = x³ – mx² + 1 tiếp xúc nhau

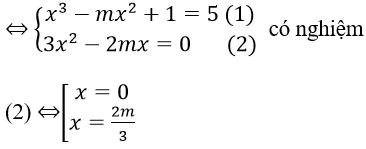
+ Với x = 0 thay vào (1) không thỏa mãn

+ Với x = 2m/3 thay vào (1) ta có: m³ = -27 ⇔ m = -3

Bài 40: Cho hàm số 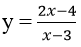có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H) với trục hoành là:

A. y = 2x – 4

B. y = 3x + 1

C. y = - 2x + 4

D. y = 2x

Lời giải:

Đáp án: C

Chọn C

Giao điểm của (H) với trục hoành là A(2;0). Ta có:

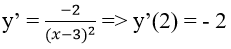
Phương trình tiếp tuyến cần tìm là y = -2(x – 2) = -2x + 4