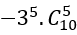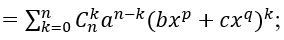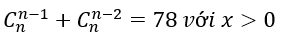Xác định hệ số, số hạng trong khai triển nhị thức Niu-tơn - Toán lớp 11

---

Xác định hệ số, số hạng trong khai triển nhị thức Niu-tơn

Với Xác định hệ số, số hạng trong khai triển nhị thức Niu-tơn Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Xác định hệ số, số hạng trong khai triển nhị thức Niu-tơn từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải & Ví dụ

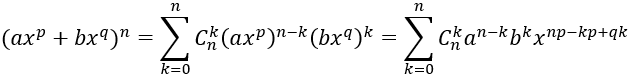
Số hạng chứa x^m ứng với giá trị k thỏa mãn: np – pk + qk = m.

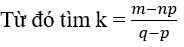
Vậy hệ số của số hạng chứa x^m là: 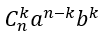với giá trị k đã tìm được ở trên.

Nếu k không nguyên hoặc k > n thì trong khai triển không chứa x^m , hệ số phải tìm bằng 0.

Chú ý: Xác định hệ số của số hạng chứa x^m trong khai triển P(x) = (a + bx^p + cx^q)ⁿ

P(x) = (a + bx^p + cx^q)ⁿ được viết dưới dạng a₀ + a₁x + ...+ a_2nx²ⁿ

Ta làm như sau:

* Viết P(x) = (a + bx^p + cx^q)ⁿ

* Viết số hạng tổng quát khi khai triển các số hạng dạng (bx^p+cx^q)^k thành một đa thức theo luỹ thừa của x.

* Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của x^m.

Chú ý: Để xác định hệ số lớn nhất trong khai triển nhị thức Niutơn

Ta làm như sau:

* Tính hệ số a_k theo k và n;

* Giải bất phương trình a_k-1 ≤ a_k với ẩn số k;

* Hệ số lớn nhất phải tìm ứng với số tự nhiên k lớn nhất thoả mãn bất phương trình trên.

Ví dụ minh họa

Bài 1: Tìm hệ số của x⁵ trong khai triển đa thức của: x(1-2x)⁵+x² (1+3x)¹⁰

Đáp án và hướng dẫn giải

Đặt f(x)=x(1-2x)⁵+x² (1+3x)¹⁰

Ta có :

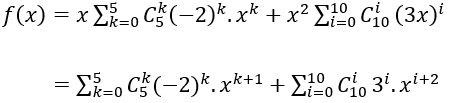
Vậy hệ số của x⁵ trong khai triển đa thức của f(x) ứng với k = 4 và i = 3 là:

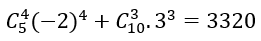
Bài 2: Đa thức P(x) =(1+3x+2x²)¹⁰=a₀ + a₁ x + ⋯ + a₂₀ x²⁰. Tìm a₁₅

Đáp án và hướng dẫn giải

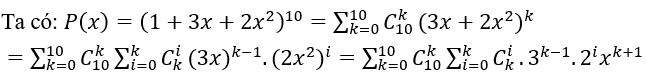
với 0 ≤ i ≤ k ≤ 10. Do đó k + i = 15 với các trường hợp

k=10, i=5 hoặc k=9, i=6 hoặc k=8, i=7

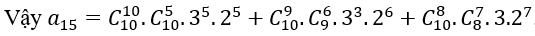
Bài 3: Tìm hệ số không chứa x trong các khai triển sau (x³ - (2/x))ⁿ, biết rằng

Đáp án và hướng dẫn giải

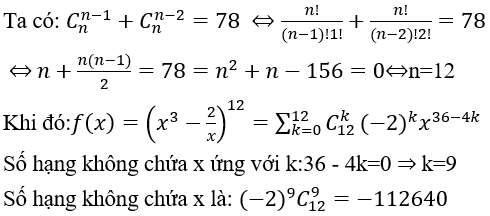
B. Bài tập vận dụng

Bài 1: Tìm hệ số cuả x⁸ trong khai triển đa thức f(x)=[1+x² (1-x)]⁸

Lời giải:

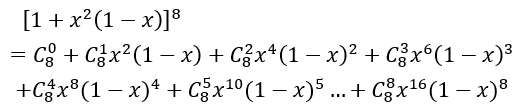
Trong khai triển trên ta thấy bậc của x trong 3 số hạng đầu nhỏ hơn 8, bậc của x trong 4 số hạng cuối lớn hơn 8. Do đó x⁸ chỉ có trong số hạng thứ tư, thứ năm với hệ số tương ứng là:

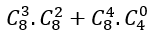
Vậy hệ số cuả x⁸ trong khai triển đa thức [1+x² (1-x)]⁸ là:

a₈ = 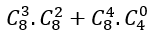= 238.

Bài 2: Đa thức P(x) = (1 + 3x + 2x²)¹⁰ = a₀ + a₁ x+⋯+a₂₀ x²⁰.. Tìm a₁₅

Lời giải:

Ta có:

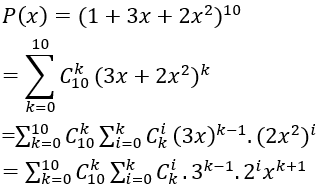
với 0 ≤ i ≤ k ≤ 10. Do đó k+i = 15 với các trường hợp

k=10, i=5 hoặc k=9, i=6 hoặc k=8, i=7

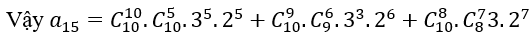
Bài 3: Trong khai triển (2a-b)⁵, hệ số của số hạng thứ bằng bao nhiêu?

Lời giải:

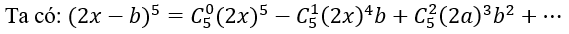
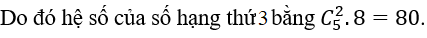
Bài 4: Trong khai triển nhị thức (a+2)ⁿ⁺⁶,(n ϵ Z). Có tất cả số hạng. Vậy n bằng bao nhiêu?

Lời giải:

Trong khai triển (a+2)⁽ⁿ⁺⁶⁾,(n ϵ N) có tất cả n+7 số hạng.

Do đó n+7 =17 ⇔ n=10.

Bài 5: Trong khai triển (3x²-y)¹⁰, hệ số của số hạng chính giữa là bao nhiêu?

Lời giải:

Trong khai triển (3x²-y)¹⁰ có tất cả 11 số hạng nên số hạng chính giữa là số hạng thứ 6.

Vậy hệ số của số hạng chính giữa là .