Chứng minh định lí Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn

Chứng minh định lí “Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn” thông qua việc giải bài tập sau đây:

Giải vở bài tập Toán 7 Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh

Câu 1 trang 83 vở bài tập Toán lớp 7 Tập 2:Chứng minh định lí “Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn” thông qua việc giải bài tập sau đây:

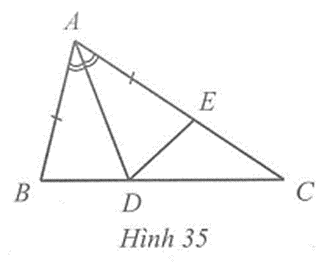
Cho tam giác ABC có AB < AC. Tia phân giác của góc BAC cắt cạnh BC tại điểm D. Điểm E thuộc cạnh AC thoả mãn AE = AB. Chứng minh:

a) ∆ABD = ∆AED;

b) $\hat{B}>\hat{C}.$

Lời giải:

a) Xét hai tam giác ABD và AED, ta có:

AB = AE (giả thiết)

$\widehat{\mathrm{DAB}}$= $\widehat{\mathrm{DAE}}$ (vì AD là tia phân giác góc $\widehat{\mathrm{BAC}}$)

AD là cạnh chung

Suy ra: ∆ABD = ∆AED (c.g.c)

b) Từ câu a) suy ra $\hat{B}=\hat{E}$(1)

Ta có: $\widehat{\mathrm{AED}}$+ $\widehat{\mathrm{DEC}}$ = 180^o (hai góc kề bù)

$\widehat{\mathrm{EDC}}$+ $\hat{C}$+ $\widehat{\mathrm{DEC}}$ = 180^o (tổng ba góc của một tam giác).

Suy ra: $\widehat{\mathrm{AED}}$ = $\widehat{\mathrm{EDC}}$+ $\hat{C}$. Do đó $\widehat{\mathrm{AED}}$ > $\hat{C}$(2)

Từ (1) và (2), ta có $\hat{B}$> $\hat{C}$.