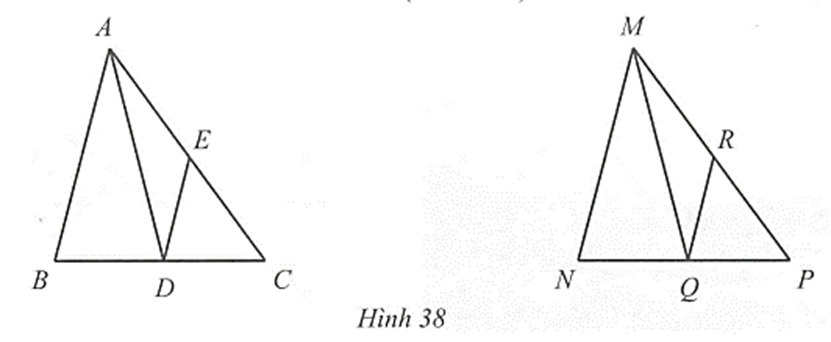
Cho tam giác ABC và tam giác MNP. Gọi D, E lần lượt là trung điểm của BC và CA

Cho ∆ABC và ∆MNP. Gọi D, E lần lượt là trung điểm của BC và CA; Q, R lần lượt là trung điểm của NP và PM. Chứng minh

Giải vở bài tập Toán 7 Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh

Câu 4 trang 86 vở bài tập Toán lớp 7 Tập 2:Cho ∆ABC và ∆MNP. Gọi D, E lần lượt là trung điểm của BC và CA; Q, R lần lượt là trung điểm của NP và PM. Chứng minh

a) AD = MQ;

b) DE = QR.

Lời giải:

Vì ∆ABC = ∆MNP nên: BC = NP, AC = MP (hai cạnh tương ứng), $\hat{C}$= $\hat{P}$(hai góc tương ứng)

a) Ta có D, Q lần lượt là trung điểm của BC và NP nên CD = $\frac{1}{2}$BC, PQ = $\frac{1}{2}$NP.

Mà BC = BP nên CD = PQ.

Xét hai tam giác ACD và MPQ, ta có AC = MP, $\hat{C}$ = $\hat{P}$, CD = PQ

Suy ra ∆ACD = ∆MPQ (c.g.c). Do đó AD = MQ (hai cạnh tương ứng).

b) Ta có E, R lần lượt là trung điểm của AC và MP nên CE = $\frac{1}{2}$AC, PR = $\frac{1}{2}$MP.

Mà AC = MP nên CE = PR

Xét hai tam giác ECD và RPQ, ta có: EC = PR, $\hat{C}$= $\hat{P}$, CD = PQ

Suy ra, ∆ECD = ∆RPQ (c.gc). Do đó DE = QR (hai cạnh tương ứng).