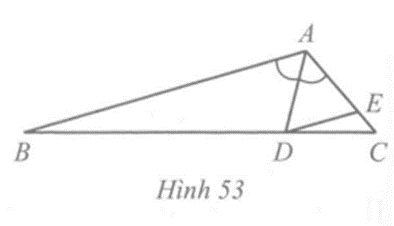
Cho tam giác ABC có góc A = 120 độ. Tia phân giác của góc A cắt BC tại D

Cho tam giác ABC có = 120. Tia phân giác của góc A cắt BC tại D. Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh tam giác ADE đều.

Giải vở bài tập Toán 7 Bài 7: Tam giác cân

Câu 2 trang 94 vở bài tập Toán lớp 7 Tập 2:Cho tam giác ABC có $\hat{A}$ = 120^o. Tia phân giác của góc A cắt BC tại D. Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh tam giác ADE đều.

Lời giải:

Vì AD là tia phân giác của góc BAC, nên

$\widehat{\mathrm{BAD}}$= $\widehat{\mathrm{CAD}}$ = $\frac{1}{2}\widehat{BAC}$ = 60^o

Tức là $\widehat{\mathrm{DAE}}$ = 60°

Ta có DE // AB (giả thiết) nên $\widehat{ADE}$= $\widehat{DAB}$ (hai góc so le trong) do đó $\widehat{ADE}$ = 60°.

Vậy tam giác ADE có $\widehat{\mathrm{DAE}}$= $\widehat{ADE}$ = 60^o nên tam giác ADE là tam giác cân và có một góc bằng 60° nên tam giác ADE là tam giác đều.