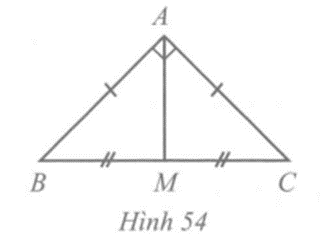
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân
Giải vở bài tập Toán 7 Bài 7: Tam giác cân
Câu 3 trang 94 vở bài tập Toán lớp 7 Tập 2:Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân
Lời giải:
Vì tam giác ABC vuông cân tại A nên ˆB = 45°.
Xét hai tam giác AMB và AMC, ta có:
AB = AC (vì tam giác ABC cân tại A);
MB = MC (vì M là trung điểm của BC)
AM là cạnh chung.
Suy ra ∆AMB = ∆AMC (c.c.c). Do đó ^AMB = ^AMC.
Mà ^AMB + ^AMC = 180o (hai góc kề bù) nên ^AMB = ^AMC = 90o
Từ đó ∆AMB vuông tại M có ˆB = 45o, nên ^BAM = 45°.
Suy ra ^BAM = ˆB
Vậy tam giác MAB là tam giác vuông cân.