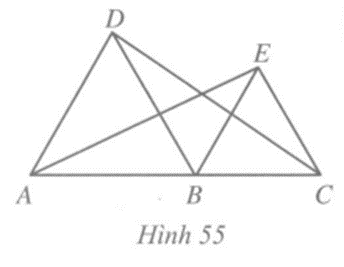
Trong Hình 55, cho biết các tam giác ABD và BCE là các tam giác đều và A, B, C thẳng hàng

Trong , cho biết các tam giác ABD và BCE là các tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:

Giải vở bài tập Toán 7 Bài 7: Tam giác cân

Câu 4 trang 94 vở bài tập Toán lớp 7 Tập 2:Trong Hình 55, cho biết các tam giác ABD và BCE là các tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:

a) AD // BE, BD // CE.

b) $\widehat{ABE}=\widehat{DBC}$ = 120^o.

c) AE = CD.

Lời giải:

a) Vì tam giác ABD và BCE là tam giác đều nên:

$\widehat{\mathrm{ABD}}$ = $\widehat{\mathrm{BAD}}$ = 60^o và $\widehat{\mathrm{BCE}}$ = $\widehat{\mathrm{CBE}}$ = 60^o .

Hai đường thẳng AD và BE cắt đường thẳng AB có hai góc đồng vị $\widehat{BAD}$, $\widehat{\mathrm{CBE}}$ thoả mãn $\widehat{BAD}$ = $\widehat{\mathrm{CBE}}$ nên AD // BE.

Hai đường thẳng BD và CE cắt đường thẳng BC có hai góc đồng vị $\widehat{\mathrm{BCE}}$, $\widehat{\mathrm{ABD}}$ thoả mãn $\widehat{\mathrm{BCE}}$ = $\widehat{\mathrm{ABD}}$ nên BD // CE.

b) Ta có: $\widehat{\mathrm{ABE}}+\widehat{\mathrm{CBE}}$ = 180^o (hai góc kề bù) và $\widehat{CBE}$ = 60°.

Suy ra $\widehat{\mathrm{ABE}}$= 180° – $\widehat{CBE}$ = 180° – 60° = 120°.

Ta có: $\widehat{DBC}$ + $\widehat{ABD}$ = 180° (hai góc kề bù) và $\widehat{ABD}$ = 60°.

Suy ra $\widehat{DBC}$ = 180° – $\widehat{ABD}$ = 180° – 60° = 120°.

Vậy $\widehat{\mathrm{ABE}}$ = $\widehat{DBC}$ = 120^o.

c) Xét hai tam giác ABE và DBC, ta có

AD = BD (do tam giác ABD đều)

$\widehat{\mathrm{ABE}}$= $\widehat{DBC}$ (chứng minh ở trên)

BE = BC (do tam giác BCE đều)

Suy ra ∆ABE = ∆DBC (c.g.c)

Do đó AE = CD (hai cạnh tương ứng).