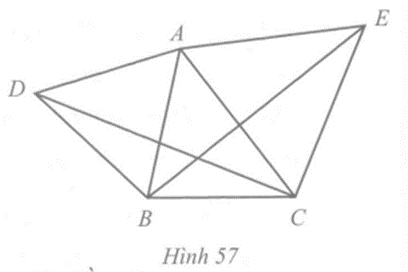
Trong hình 57 cho biết góc BAC = 45 độ, các tam giác ABD và ACE là tam giác đều

Giải vở bài tập Toán 7 Bài 7: Tam giác cân

Câu 6 trang 96 vở bài tập Toán lớp 7 Tập 2:

Trong Hình 57 cho biết $\hat{B A C}$ = 45^o, các tam giác ABD và ACE là tam giác đều.

a) Tính số đo các góc $\hat{B A E}$ , $\hat{C A D}$ ;

b) Chứng minh rằng BE = CD.

Lời giải:

a) Vì các tam giác ABD và ACE là tam giác đều nên

$\hat{B A D}$ = $\hat{C A E}$ = 60^o.

Từ đó do $\hat{B A C}$ và $\hat{C A E}$ , $\hat{B A C}$ và $\hat{B A D}$ là các cặp góc kề nhau nên

$\hat{B A E}$ = $\hat{B A C}$ + $\hat{C A E}$ = 45^o + 60⁰ = 105^o.

$\hat{C A D}$ = $\hat{C A B}$ + $\hat{B A D}$ = 45^o + 60⁰ = 105^o.

b) Xét hai tam giác ABE và ADC, ta có:

AB = AD (do tam giác ABD đều)

$\hat{B A E}$ = $\hat{C A D}$ = 105^o (chứng minh ở trên)

AE = AC (do tam giác ACE đều)

Suy ra ∆ABE = ∆ADC (c.g.c). Do đó BE = CD (hai cạnh tương ứng).