Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu

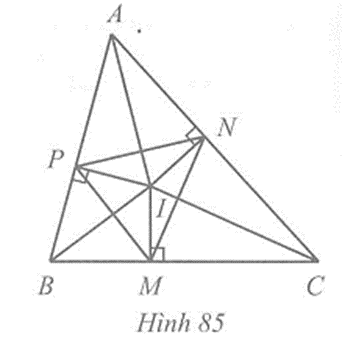
Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.

Giải vở bài tập Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác

Câu 3 trang 110 vở bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.

Lời giải:

Do điểm I là giao điểm của ba đường phân giác của tam giác ABC nên IM = IN = IP.

Xét hai tam giác vuông IAP và IAN, ta có:

IA là cạnh chung;

$\widehat{\mathrm{IAP}}$= $\widehat{\mathrm{IAN}}$(Vì I thuộc tia phân giác góc A).

Suy ra ∆IAP = ∆IAN (cạnh huyền – góc nhọn).

Do đó AP = AN (hai cạnh tương ứng).

Vì IN = IP nên I nằm trên đường trung trực của đoạn thẳng NP.

Vì AP = AN nên A nằm trên đường trung trực của đoạn thẳng NP.

Suy ra IA là đường trung trực của đoạn thẳng NP.

Chứng minh tương tự ta có: IB là đường trung trực của đoạn thẳng MP, IC là đường trung trực của đoạn thẳng MN.