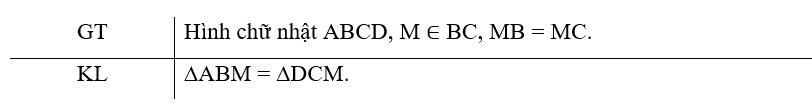Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Chứng minh rằng ∆ABM = ∆DCM
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Chứng minh rằng ∆ABM = ∆DCM.
Giải Vở thực hành Toán 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông
Bài 3 (4.22) trang 71 vở thực hành Toán lớp 7 Tập 1: Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Chứng minh rằng ∆ABM = ∆DCM.
Lời giải:
Ta thấy ABM và DCM là hai tam giác lần lượt vuông tại các đỉnh B, C và ta có:
AB = CD (hai cạnh đối của hình chữ nhật bằng nhau).
MB = MC (theo giả thiết).
Vậy ∆ABM = ∆DCM (hai cạnh góc vuông).
