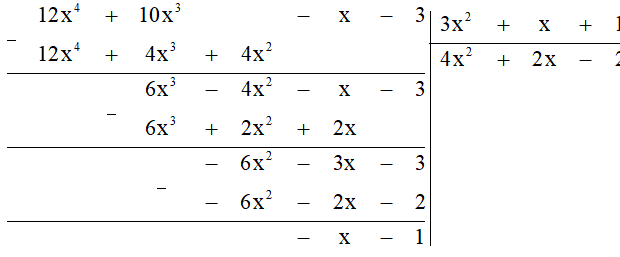Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x)

Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng: F(x) = G(x) . Q(x) + R(x).

Giải vở thực hành Toán 7 Bài 28: Phép chia đa thức một biến

Bài 5 (7.34) trang 47 vở thực hành Toán lớp 7 Tập 2: Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng: F(x) = G(x) . Q(x) + R(x).

a) F(x) = 6x⁴ - 3x³ + 15x² + 2x - 1; G(x) = 3x².

b) F(x) = 12x⁴ + 10x³ - x - 3; G(x) = 3x² + x + 1.

Lời giải:

a) Ta có:

(6x⁴ - 3x³ + 15x² + 2x - 1) : 3x² = 2x² – x + 5 (dư 2x – 1).

Do đó Q(x) = 2x² - x + 5; R(x) = 2x - 1.

Vậy F(x) = G(x)(2x² – x + 5) + 2x – 1.

b) Đặt tính chia:

Có nghĩa là F(x) : G(x) = 4x² + 2x – 2 (dư – x – 1).

Do đó Q(x) = 4x² + 2x - 2; R(x) = -x - 1.

Vậy F(x) = G(x)(4x² + 2x - 2) + (- x - 1).