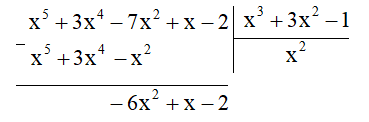Cho hai đa thức A = x^5 + 3x^4 – 7x^2 + x – 2 và B = x^3 + 3x^2 – 1

Cho hai đa thức A = x + 3x – 7x + x – 2 và B = x+ 3x – 1.

Giải vở thực hành Toán 7 Bài 28: Phép chia đa thức một biến

Bài 7 trang 48 vở thực hành Toán lớp 7 Tập 2: Cho hai đa thức A = x⁵ + 3x⁴ – 7x² + x – 2 và B = x³ + 3x² – 1.

a) Bằng cách đặt tính chia, hãy tìm thương và dư trong phép chia A cho B.

b) Em có cách nào không cần thực hiện phép chia mà vẫn tìm được đa thức dư hay không?

Lời giải:

a) Ta đặt tính chia như sau:

Vậy trong phép chia A cho B ta được thương là x² và dư là – 6x² + x – 2.

b) Không thực hiện phép chia, ta có thể tìm được thương và dư của phép chia này bằng cách biến đổi đa thức A như sau:

A = x⁵ + 3x⁴ – 7x² + x – 2

A = (x⁵ + 3x⁴ – x²) – 6x² + x – 2          (Vì – 7x² = – x² – 6x²)

A = (x³ + 3x² – 1)x² + (– 6x² + x – 2)  (Vì x⁵ + 3x⁴ – x² = (x³ + 3x² – 1)x²)

A = B . x² + (– 6x² + x – 2)

Trong đẳng thức cuối, đa thức – 6x² + x – 2 có bậc 2 nhỏ hơn bậc của B.

Điều đó chứng tỏ x² là thương và – 6x² + x – 2 là dư trong phép chia A cho B.