Tam giác ABC vuông tại đỉnh A và có góc B = 30 độ. Chứng minh rằng BC = 2AC

Tam giác ABC vuông tại đỉnh A và có . Chứng minh rằng BC = 2AC.

Giải Vở thực hành Toán 7 Bài tập cuối chương 4

Bài 8 trang 81 vở thực hành Toán lớp 7 Tập 1: Tam giác ABC vuông tại đỉnh A và có $\hat{B} = 30 °$ . Chứng minh rằng BC = 2AC.

Lời giải:

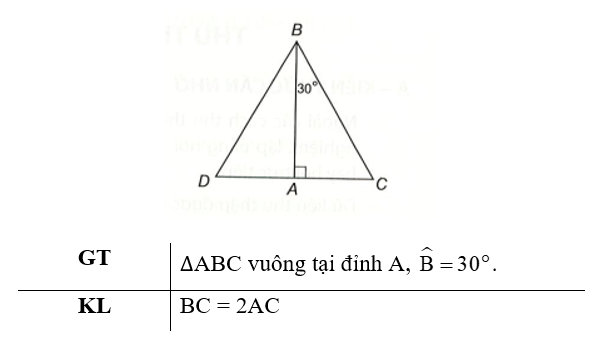
Trên tia đối của tia AC lấy điểm D sao cho AD = AC.

Tam giác ACB và tam giác ADB vuông tại A và có:

AB là cạnh chung;

AC = AD (theo cách dựng).

Vậy ∆ACB = ∆ADB (hai cạnh góc vuông). Do đó BC = BD. Vậy tam giác BCD là tam giác cân tại B. Suy ra $\hat{A B D} = \hat{A B C} = 30 °$ . Như vậy:

$\hat{C B D} = \hat{A B C} + \hat{A B C} = 2 \hat{A B C} = 60 °$ ;

$\hat{C D B} = \hat{D C B} = \frac{\hat{C D B} + \hat{D C B}}{2} = \frac{180 ° - \hat{D B C}}{2} = 60 °$ .

Vậy CBD là tam giác đều. Do đó BC = DC = 2AC (đpcm).