Giải Vở thực hành Toán 7 trang 107 Tập 2 Kết nối tri thức

---

Với Giải VTH Toán 7 trang 107 Tập 2 trong Bài tập ôn tập cuối năm Vở thực hành Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 107.

Giải Vở thực hành Toán 7 trang 107 Tập 2 Kết nối tri thức

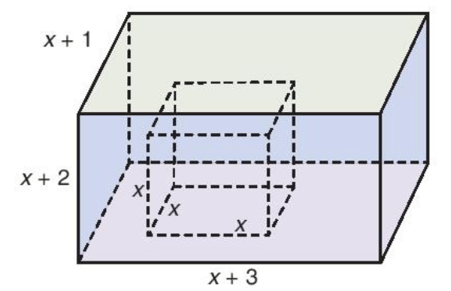
Bài 7 trang 107 vở thực hành Toán lớp 7 Tập 2: Người ta đổ đầy nước vào một cái bể hình hộp chữ nhật, sau đó nhấn chìm một khối lập phương (đặc) có độ dài các cạnh bằng x (dm) vào trong bể. Biết rằng chiều rộng, chiều dài và chiều cao của bể lần lượt bằng x + 1, x + 3 và x + 2 (xem dưới đây).

a) Tìm đa thức biểu thị thể tích nước còn lại trong bể.

b) Xác định bậc, hệ số cao nhất và hệ số tự do của đa thức trong câu a.

c) Sử dụng kết quả câu a để tính lượng nước còn lại trong bể (đơn vị: dm³) khi x = 7 (dm).

Lời giải:

a) Thể tích bể nước là:

V = (x + 1) . (x + 3) . (x + 2)

    = (x² + 4x + 3) . (x + 2)

   = x³ + 6x² + 11x + 6.

Thể tích khối lập phương (ứng với lượng nước tràn) là: V₁ = x³.

Lượng nước còn lại trong bể là:

V₂(x) = V – V₁ = 6x² + 11x + 6 (dm³).

b) V₂(x) là đa thức bậc hai, hệ số cao nhất và hệ số tự do đều bằng 6.

c) Khi x = 7, lượng nước còn lại trong bể là:

V₂(7) = 6 . 7² + 11 . 7 + 6 = 377 (dm³).

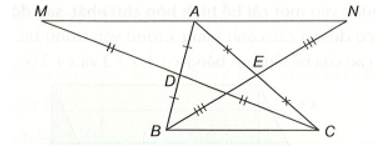
Bài 8 trang 107 vở thực hành Toán lớp 7 Tập 2: Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho DM = DC.

a) Chứng minh rằng ∆ADM = ∆BDC. Từ đó suy ra AM = BC và AM // BC.

b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho EN = EB. Chứng minh rằng AN // BC.

c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN.

Lời giải:

a) ∆ADM và ∆BDC có

AD = DB (do D là trung điểm của AB)

$\widehat{A\text{D}M}=\widehat{B\text{D}C}$ (hai góc đối đỉnh)

DM = DC (giả thiết)

Nên ∆ADM = ∆BDC (c.g.c).

Suy ra AM = BC (hai cạnh tương ứng) và $\widehat{MAD}=\widehat{CBD}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên AM // BC (dấu hiệu nhận biết hai đường thẳng song song).

b) ∆AEN và ∆CEB có:

AE = CE (E là trung điểm của AC)

$\widehat{A\text{E}N}=\widehat{CEB}$ (hai góc đối đỉnh)

EN = EB (theo giả thiết)

Nên ∆AEN = ∆CEB (c.g.c).

Suy ra $\widehat{E\text{A}N}=\widehat{ECB}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên AN // BC (dấu hiệu nhận biết hai đường thẳng song song).

c) Ta có AM // BC (chứng minh trên),

   AN // BC (chứng minh trên) nên AM và AN trùng nhau (theo tiên đề Euclid).

Từ đó suy ra ba điểm M, A, N thẳng hàng.

Ta lại có AM = BC (chứng minh trên), AN = BC (chứng minh trên – do ∆AEN = ∆CEB),

do đó AM = AN.

Từ đó suy ra A là trung điểm của đoạn MN.

Lời giải Vở thực hành Toán lớp 7 Bài tập ôn tập cuối năm Kết nối tri thức hay khác:

• Giải VTH Toán 7 trang 104 Tập 2
• Giải VTH Toán 7 trang 105 Tập 2
• Giải VTH Toán 7 trang 108 Tập 2
• Giải VTH Toán 7 trang 110 Tập 2
• Giải VTH Toán 7 trang 111 Tập 2
• Giải VTH Toán 7 trang 112 Tập 2
• Giải VTH Toán 7 trang 113 Tập 2