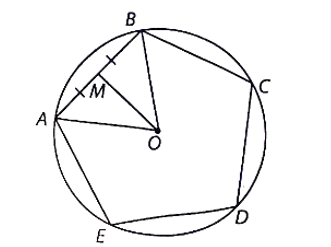
Cho ngũ giác đều ABCDE có cạnh bằng 4 cm nội tiếp một đường tròn (O)

Cho ngũ giác đều ABCDE có cạnh bằng 4 cm nội tiếp một đường tròn (O).

Giải vở thực hành Toán 9 Bài 30: Đa giác đều - Kết nối tri thức

Bài 8 trang 105 VTH Toán 9 Tập 2: Cho ngũ giác đều ABCDE có cạnh bằng 4 cm nội tiếp một đường tròn (O).

a) Tính bán kính của (O) biết rằng ta lấy cos 54° ≈ 0,59.

b) Liệt kê năm phép quay ngược chiều giữ nguyên ngũ giác đều ABCDE.

Lời giải:

Cho ngũ giác đều ABCDE có cạnh bằng 4 cm nội tiếp một đường tròn (O)

a) Ta thấy các cung nhỏ sau thỏa mãn:

$\overset{⏜}{A B} = \overset{⏜}{B C} = \overset{⏜}{C D} = \overset{⏜}{D E} = \overset{⏜}{E A} .$ Suy ra

$\hat{A O B} = s đ \overset{⏜}{A B} = \frac{360 °}{5} = 72 ° .$

Gọi M là trung điểm của AB.

Vì tam giác AOB cân tại O nên OM ⊥ AB và OM là đường phân giác của góc $\hat{A O B} .$

Suy ra $\hat{A O M} = \frac{\hat{A O B}}{2} = \frac{72 °}{2} = 36 ° .$

Như vậy $\hat{M A O} = 90 ° - \hat{A O M} = 54 ° .$

Bán kính của (O) là: $R = \frac{A M}{\cos \hat{M A O}} = \frac{2}{\cos 54 °} \approx \frac{2}{0, 59} \approx 3, 39$ (cm).

b) Năm phép quay ngược chiều giữ nguyên ngũ giác đều là các phép quay ngược chiều lần lượt 72°, 144°, 216°, 288°, 360° với tâm O.

Lời giải vở thực hành Toán 9 Bài 30: Đa giác đều hay khác: