Tam giác ABC cân tại A, đường cao AH, có AB = 5 cm, BC = 8 cm. Quay tam giác ABC
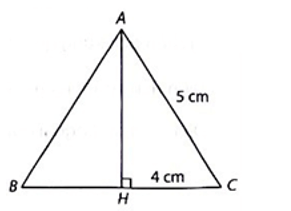
Tam giác ABC cân tại A, đường cao AH, có AB = 5 cm, BC = 8 cm. Quay tam giác ABC một vòng quanh cạnh AH ta được một hình nón.
Giải vở thực hành Toán 9 Bài 31: Hình trụ và hình nón - Kết nối tri thức
Bài 8 trang 118 VTH Toán 9 Tập 2: Tam giác ABC cân tại A, đường cao AH, có AB = 5 cm, BC = 8 cm. Quay tam giác ABC một vòng quanh cạnh AH ta được một hình nón.
a) Tính thể tích hình nón (làm tròn kết quả đến hàng phần trăm của cm3).
b) Tính diện tích toàn phần của hình nón (làm tròn kết quả đến hàng phần trăm của cm2).
Lời giải:
a) Tam giác ABC cân tại A, đường cao AH.
Suy ra H là trung điểm của BC nên HC = HB = = 4 (cm).
Tam giác AHC vuông tại H nên theo định lí Pythagore ta có:
AH2 + HC2 = AC2
AH2 + 42 = 52
AH2 = 52 – 42 = 9
AH = 3 cm.
Khi đó: R = 4 cm, h = 3 cm, l = 5 cm.
Thể tích của hình nón là:
(cm3).
b) Diện tích toàn phần của hình nón là:
(cm2).
Lời giải vở thực hành Toán 9 Bài 31: Hình trụ và hình nón hay khác: