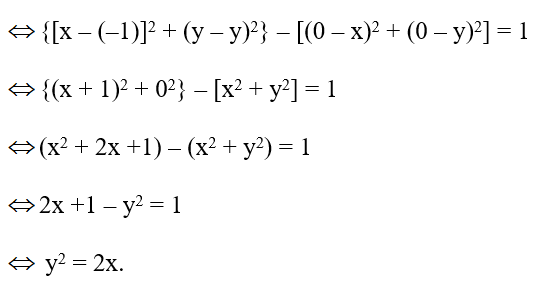Bài 7 trang 67 Chuyên đề Toán 10

Giải Chuyên đề Toán 10 Bài 4: Ba đường conic

Haylamdo biên soạn và sưu tầm lời giải Bài 7 trang 67 Chuyên đề Toán 10 trong Bài 4: Ba đường conic. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh biết cách làm bài tập Chuyên đề Toán 10.

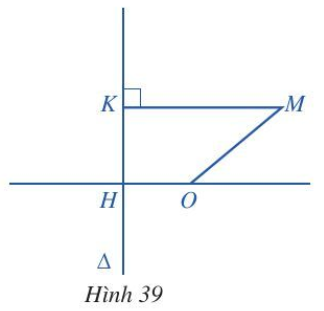
Bài 7 trang 67 Chuyên đề Toán 10: Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39).

Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên Δ. Chứng minh tập hợp các điểm M trong mặt phẳng sao cho MK² – MO² = 1 là một đường parabol.

Lời giải:

Chọn hệ trục toạ độ sao cho điểm O trùng với gốc toạ độ và trục Ox trùng với đường thẳng OH.

Giả sử M có toạ độ (x; y) thì K có toạ độ là (–1; y).

Khi đó:

MK² – MO² = 1

Vậy tập hợp các điểm M là parabol có phương trình y² = 2x.