Bài 1 trang 35 Chuyên đề Toán 12
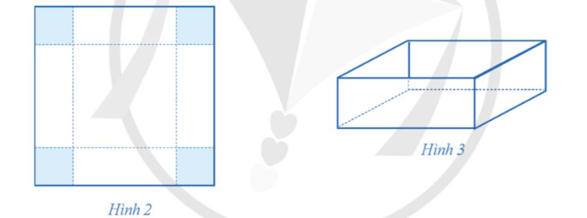
Bạn Hà có một tấm bìa hình vuông cạnh 60 cm (Hình 2). Bạn muốn làm một cái hộp đựng đồ có dạng hình hộp chữ nhật mà có thể để được vào một ngăn giá sách có dạng hình hộp chữ nhật, đáy là hình vuông cạnh bằng 37 cm, chiều cao bằng 28 cm. Bạn cắt bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập lại thành một cái hộp không nắp (Hình 3). Tìm số nguyên dương x để làm được cái hộp đựng đồ có thể tích lớn nhất.
Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn - Cánh diều
Bài 1 trang 35 Chuyên đề Toán 12: Bạn Hà có một tấm bìa hình vuông cạnh 60 cm (Hình 2). Bạn muốn làm một cái hộp đựng đồ có dạng hình hộp chữ nhật mà có thể để được vào một ngăn giá sách có dạng hình hộp chữ nhật, đáy là hình vuông cạnh bằng 37 cm, chiều cao bằng 28 cm. Bạn cắt bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập lại thành một cái hộp không nắp (Hình 3). Tìm số nguyên dương x để làm được cái hộp đựng đồ có thể tích lớn nhất.
Lời giải:
Cạnh đáy hình vuông của chiếc hộp không nắp là: 60 – 2x (cm).
Khi đó ta có: 60 – 2x < 37 hay x > 11,5.
Chiều cao của chiếc hộp không nắp là: x (cm). Khi đó ta có x < 28.
Diện tích đáy của chiếc hộp không nắp là: (60 – 2x)2 (cm2).
Thể tích của chiếc hộp không nắp là:
x.(60 – x)2 = x(3 600 – 240x + 4x2) = 3 600x – 240x2 + 4x3 (cm3).
Xét hàm số f(x) = 3 600x – 240x2 + 4x3 với 11,5 < x < 28.
Ta có f’(x) = 3 600 – 480x + 12x2.
Do đó f’(x) = 0 ⇔ x = 10 (thỏa mãn) hoặc x = 30 (không thỏa mãn).
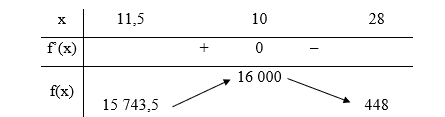
Bảng biến thiên của hàm số:
Căn cứ bảng biến thiên, ta có tại x = 10 (thỏa mãn điều kiện x là số nguyên dương).
Vậy để làm được cái hộp đựng đồ có thể tích lớn nhất thì x = 10.
Lời giải bài tập Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn hay, chi tiết khác: