Bài 4 trang 36 Chuyên đề Toán 12
Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300 km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc bơi của cá khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức
Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn - Cánh diều
Bài 4 trang 36 Chuyên đề Toán 12: Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300 km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc bơi của cá khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức
E(v) = cv3t,
trong đó c là một hằng số, E được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2020).
Lời giải:
Vận tốc của con cá hồi khi bơi ngược dòng là: v – 6 (km/h).
Thời gian để con cá hồi đó khi bơi ngược dòng 300 km là: 300v−6 (giờ).
Năng lượng tiêu hao của cá để vượt quãng đường 300 km là:
E(v)=cv3⋅300v−6=300c⋅v3v−6 (jun).
Xét hàm số E(v)=300c⋅v3v−6, v>6.
Ta có E'(v)=300c⋅3v2(v−6)−v3(v−6)2=300c⋅2v3−18v2(v−6)2=300c⋅2v2(v−9)(v−6)2.
Do đó E’(v) = 0 ⇔ v = 0 (không thỏa mãn) hoặc v = 9 (thỏa mãn do v > 0).
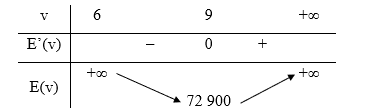
Bảng biến thiên của hàm số:
Căn cứ bảng biến thiên, ta có min(6;+∞)E(v)=E(9)=72 900 tại v = 9.
Vậy vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất là 9 km/h.
Lời giải bài tập Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn hay, chi tiết khác: