Bài 3 trang 36 Chuyên đề Toán 12
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng:
Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn - Cánh diều
Bài 3 trang 36 Chuyên đề Toán 12: Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng:
P(n) = 480 – 20n (gam)
(Nguồn: Giải tích 12 – Nâng cao, NXBGD Việt Nam, 2020).
Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
Lời giải:
Khối lượng cá thu hoạch được sau một vụ là:
n.P(n) = n.(480 – 20n) = 480n – 20n2 (gam).
Xét hàm số f(n) = 480n – 20n2 với 0 < n < 24.
Ta có: f’(n) = 480 – 40n.
Do đó f’(n) = 0 ⇔ n = 12.
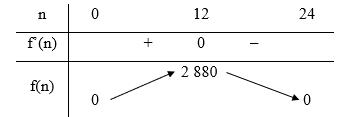
Bảng biến thiên của hàm số:
Căn cứ bảng biến thiên, ta có tại n = 12.
Vậy phải thả 12 con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất.
Lời giải bài tập Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn hay, chi tiết khác: