Bài 2 trang 35 Chuyên đề Toán 12

❮ Bài trước Bài sau ❯

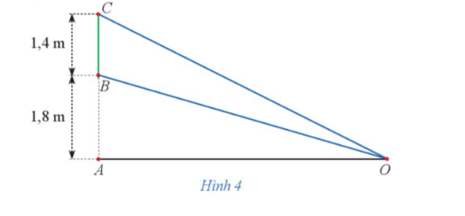
Hình 4 minh hoạ một màn hình BC có chiều cao 1,4 m được đặt thẳng đứng và mép dưới của màn hình cách mặt đất một khoảng BA = 1,8 m. Một chiếc đèn quan sát màn hình được đặt ở vị trí O trên mặt đất. Hãy tính khoảng cách AO sao cho góc quan sát BOC là lớn nhất.

Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn - Cánh diều

Bài 2 trang 35 Chuyên đề Toán 12: Hình 4 minh hoạ một màn hình BC có chiều cao 1,4 m được đặt thẳng đứng và mép dưới của màn hình cách mặt đất một khoảng BA = 1,8 m. Một chiếc đèn quan sát màn hình được đặt ở vị trí O trên mặt đất. Hãy tính khoảng cách AO sao cho góc quan sát BOC là lớn nhất.

Lời giải:

Cách 1. Để góc quan sát BOC là lớn nhất thì $\cos \hat{B O C}$ là nhỏ nhất.

Giả sử AO = x (m) (x > 0).

Bài 2 trang 35 Chuyên đề Toán 12

Do đó f’(x) = 0 ⇔ 1,96x³ – 11,2896x = 0 ⇔ x = 2,4 (vì x > 0).

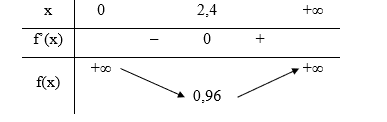
Bảng biến thiên của hàm số:

Bài 2 trang 35 Chuyên đề Toán 12

Căn cứ bảng biến thiên, ta có $\min_{(0; + \infty)} f (x) = f (2, 4) = 0, 96$ tại x = 2,4.

Vậy để góc quan sát BOC là lớn nhất thì khoảng cách AO là 2,4 mét.

Cách 2. Để góc quan sát BOC là lớn nhất thì $\tan \hat{B O C}$ là lớn nhất.

Giả sử AO = x (m) (x > 0).

Ta có $\tan \hat{B O C} = \tan (\hat{A O C} - \hat{A O B}) = \frac{\tan \hat{A O C} - \tan \hat{A O B}}{1 + \tan \hat{A O C} \cdot \tan \hat{A O B}}$

$= \frac{\frac{A C}{A O} - \frac{A B}{A O}}{1 + \frac{A C}{A O} \cdot \frac{A B}{A O}} = \frac{\frac{1, 4}{x}}{1 + \frac{1, 8 + 1, 4}{x} \cdot \frac{1, 8}{x}} = \frac{1, 4 x}{x^{2} + 5, 76} .$

Xét hàm số $f (x) = \frac{1, 4 x}{x^{2} + 5, 76}, x \in (0; + \infty) .$

Ta có: $f^{'} (x) = \frac{1, 4 \cdot (x^{2} + 5, 76) - 1, 4 x \cdot 2 x}{{(x^{2} + 5, 76)}^{2}} = \frac{- 1, 4 x^{2} + 8, 064}{{(x^{2} + 5, 76)}^{2}} .$

Do đó f’(x) = 0 ⇔ x = 2,4 (do x > 0).

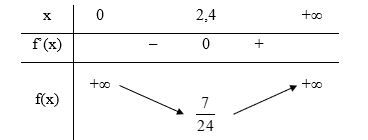
Bảng biến thiên của hàm số:

Bài 2 trang 35 Chuyên đề Toán 12

Căn cứ bảng biến thiên, ta có $\min_{(0; + \infty)} f (x) = f (2, 4) = \frac{7}{24}$ tại x = 2,4.

Vậy để góc quan sát BOC là lớn nhất thì khoảng cách AO là 2,4 mét.

Lời giải bài tập Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn hay, chi tiết khác:

Chuyên đề học tập Toán 12

Bài 2 trang 35 Chuyên đề Toán 12

Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn - Cánh diều

Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Cánh diều hay, chi tiết khác: