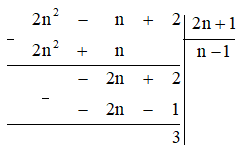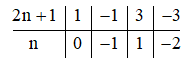Bộ đề thi Học kì 2 Toán lớp 7 năm 2023 (15 đề - Sách mới )

---

Bộ đề thi Học kì 2 Toán lớp 7 năm 2023 (15 đề - Sách mới)

Tải đề thi

Haylamdo biên soạn và sưu tầm Bộ đề thi Học kì 2 Toán lớp 7 năm 2023 có đáp án Chân trời sáng tạo, Kết nối tri thức, Cánh diều được tổng hợp chọn lọc từ đề thi môn Toán 7 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 7.

Xem thử Đề Toán 7 CK2 KNTT Xem thử Đề Toán 7 CK2 CD Xem thử Đề Toán 7 CK2 CTST

Chỉ 100k mua trọn bộ Đề thi Toán 7 Cuối kì 2 (mỗi bộ sách) bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

• Đề thi Học kì 2 Toán 7 Kết nối tri thức có đáp án (4 đề)

  Xem đề thi

• Đề thi Học kì 2 Toán 7 Cánh diều có đáp án (4 đề)

  Xem đề thi

• Đề thi Học kì 2 Toán 7 Chân trời sáng tạo có đáp án (4 đề)

  Xem đề thi

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Kết nối tri thức

Năm học 2023

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 1)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Từ đẳng thức 2.15 = 6.5 lập được tỉ lệ thức nào sau đây?

A. $\frac{5}{15}=\frac{6}{2}$;

B. $\frac{2}{5}=\frac{6}{15}$;

C. $\frac{2}{15}=\frac{5}{6}$;

D. $\frac{5}{6}=\frac{15}{2}$.

Câu 2. Giá trị nào của x thỏa mãn $\frac{x-1}{6}=\frac{x-5}{7}$?

A. x = –27;

B. x = –23;

C. x = 23;

D. x = 27.

Câu 3. Đại lượng y tỉ lệ nghịch với đại lượng x nếu:

A. x = ay với hằng số a ≠ 0;

B. $y=\frac{a}{x}$ với hằng số a ≠ 0;

C. y = ax với hằng số a ≠ 0;

D. $y=\frac{x}{a}$ với hằng số a ≠ 0.

Câu 4. Trong các biểu thức sau, biểu thức nào là biểu thức số?

A. 3² − 4;

B. x – 6 + y;

C. x² + x;

D. $\frac{1}{x}+x+1$.

Câu 5. Cho hai biểu thức: E = 2(a + b) – 4a + 3 và F = 5b – (a – b).

Khi a = 5 và b = –1. Chọn khẳng định đúng:

A. E = F;

B. E > F;

C. E < F;

D. E ≈ F.

Câu 6. Giá trị x = ‒ 1 là nghiệm của đa thức nào sau đây?

A. M(x) = x – 1;

B. N(x) = x + 1;

C. P(x) = x;

D. Q(x) = – x.

Câu 7. Trong một phép thử, bạn An xác định được biến cố M, biến cố N có xác suất lần lượt là $\frac{1}{3}$ và $\frac{1}{2}$. Hỏi biến cố nào có khả năng xảy ra thấp hơn?

A. Biến cố M;

B. Biến cố N;

C. Cả hai biến cố M và N đều có khả năng xảy ra bằng nhau;

D. Không thể xác định được.

Câu 8. Khẳng định nào sau đây là đúng?

A. Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh nhỏ hơn;

B. Trong một tam giác, góc đối diện với cạnh nhỏ hơn là góc lớn hơn;

C. Trong một tam giác vuông, cạnh huyền là cạnh nhỏ nhất;

D. Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

Câu 9. Cho ∆ABC có AB > BC > AC. Chọn khẳng định sai:

A. AB < BC – AC;

B. AB > BC – AC;

C. AC > AB – BC;

D. AC < AB + BC.

Câu 10. Cho tam giác ABC. Ba đường trung trực của tam giác ABC cùng đi qua một điểm M. Khẳng định nào sau đây là đúng?

A. M cách đều ba đỉnh của tam giác ABC;

B. M cách đều ba cạnh của tam giác ABC;

C. M là trọng tâm tam giác ABC;

D. M là trực tâm tam giác ABC.

Câu 11. Hình hộp chữ nhật, hình lập phương không có chung đặc điểm nào dưới đây?

A. Các cạnh bằng nhau;

B. Các mặt đáy song song;

C. Các cạnh bên song song với nhau;

D. Có 8 đỉnh.

Câu 12. Một hình hộp chữ nhật có diện tích xung quanh là 180 cm², độ dài hai cạnh đáy là 8 cm và 10 cm. Chiều cao của hình hộp chữ nhật đó là

A. 2 cm;

B. 4 cm;

C. 5 cm;

D. 10 cm.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm) Cho đa thức A(x) = –11x⁵ + 4x – 12x² + 11x⁵ + 13x² – 7x + 2.

a) Thu gọn, sắp xếp đa thức A(x) theo số mũ giảm dần của biến rồi tìm bậc, hệ số cao nhất của đa thức.

b) Tìm đa thức M(x) sao cho M(x) = A(x).B(x), biết B(x) = x – 1.

c) Tìm nghiệm của đa thức A(x).

Bài 2. (1,0 điểm) Ba đội công nhân cùng chuyển một khối lượng gạch như nhau. Thời gian để đội thứ nhất, đội thứ hai và đội thứ ba làm xong công việc lần lượt là 2 giờ, 3 giờ, 4 giờ. Tính số công nhân tham gia làm việc của mỗi đội, biết rằng số công nhân của đội thứ ba ít hơn số công nhân của đội thứ hai là 5 người và năng suất lao động của các công nhân là như nhau.

Bài 3. (1,0 điểm) Chọn ngẫu nhiên một số trong tập hợp M = {2; 3; 5; 6; 8; 9}.

a) Trong các biến cố sau, biến cố nào là biến cố chắc chắn? Biến cố nào là biến cố không thể và biến cố nào là biến cố ngẫu nhiên?

A: “Số được chọn là số nguyên tố”;

B: “Số được chọn là số có một chữ số”;

C: “Số được chọn là số tròn chục”.

b) Tính xác suất của biến cố A.

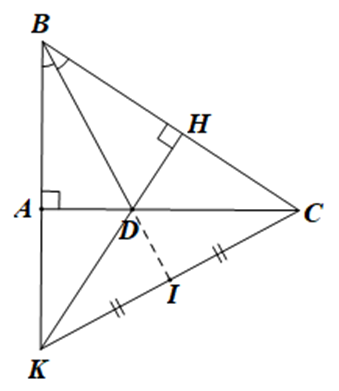
Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A, đường phân giác BD (D∈AC). Từ D kẻ DH vuông góc với BC.

a) Chứng minh ΔABD = ΔHBD.

b) So sánh AD và DC.

c) Gọi K là giao điểm của đường thẳng AB và DH, I là trung điểm của KC. Chứng minh 3 điểm B, D, I thẳng hàng.

Bài 5. (0,5 điểm) Tìm các giá trị nguyên của n để 2n² – n + 2 chia hết cho 2n + 1.

ĐÁP ÁN ĐỀ SỐ 01

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Bảng đáp án:

Hướng dẫn giải phần trắc nghiệm

Câu 1.

Đáp án đúng là: B

Từ đẳng thức 2.15 = 6.5 ta lập được tỉ lệ thức là: $\frac{2}{5}=\frac{6}{15}$.

Câu 2.

Đáp án đúng là: B

Từ $\frac{x-1}{6}=\frac{x-5}{7}$ suy ra:

7.(x – 1) = 6.(x – 5)

7x – 7 = 6x – 30

x = –23

Vậy x = –23.

Câu 3.

Đáp án đúng là: B

Khái niệm hai đại lượng tỉ lệ nghịch:

Nếu đại lượng y liên hệ với đại lượng x theo công thức $y=\frac{a}{x}$ hay xy = a (với a là một hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.

Câu 4.

Đáp án đúng là: A

Biểu thức 3² − 4 là biểu thức chứa các số nên là biểu thức số.

Biểu thức x – 6 + y; x² + x; $\frac{1}{x}+x+1$ có chứa chữ nên không là biểu thức số.

Câu 5.

Đáp án đúng là: B

Thay a = 5 và b = –1 vào biểu thức E, ta được:

E = 2 . [5 + (−1)] – 4 . 5 + 3

= 2 . 4 – 4 . 5 + 3

= 8 – 20 + 3

= –9.

Thay a = 5 và b = –1 vào biểu thức F, ta được:

F = 5 . (–1) – [5 – (–1)]

= –5 – (5 + 1)

= –5 – 6

= –11

Vì –9 > –11 nên E > F.

Vậy ta chọn phương án B.

Câu 6.

Đáp án đúng là: B

Thay x = ‒ 1 lần lượt vào các đa thức ta thấy N(‒1) = 0, do đó x = ‒ 1 là nghiệm của đa thức N(x).

Câu 7.

Đáp án đúng là: A

Vì $\frac{1}{3}<\frac{1}{2}$ nên xác suất xảy ra biến cố M nhỏ hơn xác suất xảy ra biến cố N.

Do đó biến cố M có khả năng xảy ra thấp hơn biến cố N.

Câu 8.

Đáp án đúng là: D

Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn; góc đối diện với cạnh nhỏ hơn là góc nhỏ hơn.

Trong một tam giác vuông, cạnh huyền là cạnh lớn nhất.

Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

Vậy ta chọn phương án D.

Câu 9.

Đáp án đúng là: A

Ta có AB > BC – AC, nên B đúng;

AC > AB – BC, nên C đúng.

AC < AB + BC, nên D đúng;

AB < BC – AC, nên A sai.

Vậy ta chọn phương án A.

Câu 10.

Đáp án đúng là: A

Ba đường trung trực của tam giác ABC cùng đi qua một điểm M, điểm M này cách đều ba đỉnh của tam giác ABC.

Câu 11.

Đáp án đúng là: A

Chỉ có hình lập phương có tất cả các cạnh bằng nhau. Vậy hình hộp chữ nhật, hình lập phương không có chung đặc điểm các cạnh bằng nhau.

Câu 12.

Đáp án đúng là: C

Chu vi đáy của hình hộp chữ nhật là: 2 . (8 + 10) = 36 (cm).

Chiều cao của hình hộp chữ nhật đó là: 180 : 36 = 5 (cm).

PHẦN II. TỰ LUẬN (7,0 điểm)

Hướng dẫn giải phần tự luận

Bài 1. (2,0 điểm)

a) Ta có:

A(x) = –11x⁵ + 4x – 12x² + 11x⁵ + 13x² – 7x + 2

= x² – 3x + 2.

Đa thức A(x) có bậc là 2 và hệ số cao nhất là 1.

b) M(x) = A(x).B(x)

= (x² – 3x + 2).(x – 1)

= x.(x² – 3x + 2) – 1.(x² – 3x + 2)

= x³ – 3x² + 2x – x² + 3x – 2

= x² – 4x² + 5x – 2.

c) A(x) = 0

x² – 3x + 2 = 0

x² – x – 2x + 2 = 0

x(x – 1) – 2(x – 1) = 0

(x – 1)(x – 2) = 0

x = 1 hoặc x = 2.

Vậy đa thức A(x) có nghiệm là x ∈ {1; 2}.

Bài 2. (1,0 điểm)

Gọi số công nhân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là x, y, z.

Số công nhân của đội thứ ba ít hơn số công nhân của đội thứ hai là 5 người nên y – z = 5.

Với cùng một khối lượng công việc, số công nhân tham gia làm việc và thời gian hoàn thanh công việc của mỗi đội là hai đại lượng tỉ lệ nghịch với nhau.

Do đó, ta có 2x = 3y = 4z suy ra $\frac{x}{\frac{1}{2}}=\frac{y}{\frac{1}{3}}=\frac{z}{\frac{1}{4}}$.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

$\frac{x}{\frac{1}{2}}=\frac{y}{\frac{1}{3}}=\frac{z}{\frac{1}{4}}=\frac{y-z}{\frac{1}{3}-\frac{1}{4}}=\frac{5}{\frac{1}{12}}=60$.

Từ đó suy ra $x=60.\frac{1}{2}=30$ ,$y=60.\frac{1}{3}=20$, $z=60.\frac{1}{4}=15$.

Vậy số công nhân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là 30 người, 20 người, 15 người.

Bài 3. (1,0 điểm) M = {2; 3; 5; 6; 8; 9}.

a) Tập hợp M gồm có số nguyên tố và hợp số nên biến cố A là biến cố ngẫu nhiên.

Trong tập hợp M, tất cả các số đều là số có một chữ số nên biến cố B là biến cố chắc chắn.

Trong tập hợp M, không có số nào là số tròn chục nên biến cố C là biến cố không thể.

b) Trong tập hợp M gồm 6 số, có 3 số là số nguyên tố, đó là số 2; 3; 5.

Xác suất của biến cố A là: $\frac{3}{6}=\frac{1}{2}$.

Bài 4. (2,5 điểm)

a) Xét DABD và ΔHBD có:

$\widehat{BAD}=\widehat{BHD}=90°$,

BD là cạnh chung,

$\widehat{ABD}=\widehat{HBD}$ (do BD là tia phân giác của $\widehat{ABD}$).

Do đó ΔABD = ΔHBD (cạnh huyền – góc nhọn).

b) Từ ΔABD = ΔHBD (câu a) suy ra AD = HD (hai cạnh tương ứng)

Xét ΔDHC vuông tại H có DC là cạnh huyền nên DC là cạnh lớn nhất

Do đó DC > HD nên DC > AD.

c) Xét ΔBKC có CA ⊥ BK, KH ⊥ BC và CA cắt KH tại D

Do đó D là trực tâm của DBKC, nên BD ⊥ KC (1)

Gọi J là giao điểm của BD và KC.

Xét $∆$BKJ và $∆$BCJ có:

$\widehat{BJK}=\widehat{BJC}=90°$,

BJ là cạnh chung,

$\widehat{KBJ}=\widehat{CBJ}$ (do BJ là tia phân giác của $\widehat{ABD}$).

Do đó ΔBKJ = ΔBCJ (cạnh góc vuông – góc nhọn kề)

Suy ra KJ = CJ (hai cạnh tương ứng)

Hay J là trung điểm của KC.

Mà theo bài I là trung điểm của KC nên I và J trùng nhau.

Do đó ba điểm B, D, I thẳng hàng.

Bài 5. (0,5 điểm)

Thực hiện phép chia đa thức 2n² – n + 2 cho đa thức 2n + 1 như sau:

Để 2n² – n + 2 chia hết cho 2n + 1 thì (2n + 1) ∈ Ư(3) = {1; ‒1; 3; ‒3}.

Ta có bảng sau:

Vậy n ∈ {–2; –1; 0; 1}.

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Cánh diều

Năm học 2023

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 2)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Bảng sau cho biết số con của 30 gia đình trong khu dân cư:

Điểm không hợp lí trong bảng thống kê trên là

A. Số con trong một gia đình;

B. Số gia đình trong khu dân cư;

C. Tổng số con trong gia đình;

D. Tổng số gia đình được lấy dữ liệu.

Câu 2. Biểu đồ sau cho biết Tổng sản phẩm Quốc nội (GDP) Việt Nam qua các năm:

Biết đóng góp của khu vực kinh tế Công nghiệp và xây dựng vào GDP Việt Nam năm 2019 là 50%. Theo em, khu vực kinh tế này đóng góp bao nhiêu tỉ đô la?

A. 130,5 tỉ đô la;

B. 132,5 tỉ đô la;

C. 134,5 tỉ đô la;

D. 136,5 tỉ đô la.

Câu 3. Gieo hai con xúc xắc và thấy cả hai con xúc xắc đều xuất hiện mặt có số chấm là số chẵn. Trong các biến cố sau, biến cố nào là biến cố chắc chắn?

A. A: “Tổng số chấm trên cả hai con xúc xắc là một số chia 3 dư 1”;

B. B: “Tổng số chấm trên cả hai con xúc xắc là một số chia hết cho 5”;

C. C: “Tổng số chấm trên cả hai con xúc xắc là số chẵn”;

D. D: “Tổng số chấm trên cả hai con xúc xắc là một số lẻ”.

Câu 4. Trong một hộp chứa 15 quả bóng có kích thước và trọng lượng như nhau được đánh số từ 1 đến 15. Lấy ngẫu nhiên 1 quả bóng từ trong hộp. Cho biến cố F: “Lấy được quả bóng đánh số chia hết cho 9”. Xác suất của biến cố F là

A. $P\left(F\right)=\frac{1}{15}$;

B. $P\left(F\right)=\frac{2}{15}$;

C. $P\left(F\right)=\frac{1}{5}$;

D. $P\left(F\right)=\frac{1}{2}$.

Câu 5. Biểu thức x³ + 8 được phát biểu bằng lời là

A. Tổng của x lập phương và 8;

B. Lập phương của tổng x và 8;

C. Ba lần tổng của x và 8;

D. Tổng của ba lần x và 8.

Câu 6. Giá trị của biểu thức: xy(x + y) + (x – y)² tại x = – 4 và y = 2 là

A. 52;

B. 20;

C. – 20;

D. – 52.

Câu 7. Hệ số cao nhất của đa thức N(x) = –x⁴ + 3x + 5 là:

A. –1;

B. 1;

C. 3;

D. 5.

Câu 8. Trong các số sau, số nào là nghiệm của đa thức A(x) = x² – 4?

A. –4;

B. 4;

C. 2;

D. 16.

Câu 9. Cho tam giác ABC có $\hat{A}=60°,\hat{B}=x,\hat{C}=2x.$

Số đo x là bao nhiêu và tam giác ABC là tam giác gì?

A. x = 30° và tam giác ABC là tam giác cân

B. x = 40° và tam giác ABC là tam giác nhọn;

C. x = 80° và tam giác ABC là tam giác tù;

D. x = 90 và tam giác ABC là tam giác vuông.

Câu 10. Cho tam giác ABC có AB < AC. Khẳng định nào dưới đây đúng?

A. $\hat{C}>\hat{B}$;

B. $\hat{C}=\hat{B}$;

C. $\hat{C}<\hat{B}$;

D. $\hat{C}\ge \hat{B}$.

Câu 11. Chọn câu sai?

A. Tam giác vuông có hai cạnh góc vuông bằng nhau được gọi là tam giác vuông cân;

B. Tam giác đều có ba góc bằng nhau và bằng 60°;

C. Hai góc nhọn của tam giác vuông cân bằng nhau và bằng 60°;

D. Một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Câu 12. Nhận xét nào dưới đây sai?

A. Ba đường phân giác của một tam giác cùng đi qua một điểm;

B. Giao điểm ba đường phân giác của một tam giác cách đều ba đỉnh của tam giác đó;

C. Mỗi tam giác có ba đường phân giác;

D. Trong tam giác ABC, tia phân giác của góc A cắt BC tại D. Khi đó AD được gọi là đường phân giác của tam giác ABC.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm) Một đội tình nguyện viên tham gia chống dịch Covid – 19 gồm 40 thành viên đến từ các vùng miền được thống kê trong bảng sau:

a) Lập bảng thống kê tỉ lệ phần trăm số tình nguyện viên tham gia của mỗi vùng miền trong đội tình nguyện viên đó.

b) Vẽ biểu đồ biểu diễn tỉ lệ phần trăm đã tính ở câu a.

c) Chọn ngẫu nhiên một thành viên của đội. Tính xác suất của mỗi biến cố sau:

A: “Thành viên được chọn đến từ vùng Tây Nguyên hoặc Đồng bằng sông Hồng”.

B: “Thành viên được chọn không đến từ vùng Đồng bằng sông Cửu Long”.

Bài 2. (2,0 điểm) Cho đa thức A(x) = – 11x⁵ + 4x³ + 12x² + 11x⁵ – 13x² + 7x + 2.

a) Thu gọn và sắp xếp đa thức A(x) theo số mũ giảm dần của biến.

b) Xác định bậc và hệ số cao nhất của đa thức A(x).

c) Tìm đa thức M(x) sao cho M(x) = A(x) – B(x) biết B(x) = –10 + 2x³ + 3x.

d) Tính M(–1) + M(0).

Bài 3. (3,0 điểm) Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AC, điểm E trên cạnh AC sao cho BD = CE.

a) Chứng minh rằng: AD = AE và $∆$ABE = $∆$ACD.

b) Chứng minh rằng: AI là đường phân giác của góc BAC.

c) Tìm vị trí của hai điểm D và E sao cho BD = DE = EC. Khi đó tìm vị trí của điểm I.

Bài 4. (0,5 điểm) Tìm giá trị nguyên của x để đa thức 4x³ – 4x² – x + 4 chia hết cho đa thức 2x + 1.

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Chân trời sáng tạo

Năm học 2023

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 3)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Chọn câu đúng. Với điều kiện các tỉ số đều có nghĩa thì từ $\frac{x}{y}=\frac{u}{v}$ ta có

A. $\frac{x}{y}=\frac{x+u}{y+v}$;

B. $\frac{x}{y}=\frac{x+u}{y-v}$;

C. $\frac{x}{y}=\frac{x-u}{y+v}$;

D. $\frac{x}{y}=\frac{x-u}{y.v}$.

Câu 2. Giả sử x và y là hai đại lượng tỉ lệ thuận, x₁; x₂ là hai giá trị khác nhau của x và y₁; y₂ là hai giá trị tương ứng của y. Biết y₁ – x₁ = 7 và x₂ = – 4; y₂ = 3, giá trị của x₁; y₁ là

A. x₁ = –28; y₁ = 21;

B. x₁ = –3; y₁ = 4;

C. x₁ = –4; y₁ = 3;

D. x₁ = 4; y₁ = –3.

Câu 3. Cho a, b là các số đã biết không thay đổi giá trị. Các biến trong biểu thức đại số ax + by là

A. a; b;

B. a; b; x; y;

C. x; y;

D. a; x.

Câu 4. Giá trị của biểu thức x + 2x²y – y² tại x = –1 và y = –1 là

A. 0;

B. –4;

C. 2;

D. –2.

Câu 5. Chọn khẳng định đúng.

Xét tam giác ABC có:

A. AB + BC < AC;

B. AC – BC > AB;

C. AB + BC > AC;

D. AB + BC = AC.

Câu 6. Cho tam giác ABC có AH ⊥ BC (H ∈ BC) thì

A. AB > AH;

B. BH = CH;

C. AB < AC;

D. AH < BC.

Câu 7. Cho tam giác ABC với hai đường trung tuyến BM và CN cắt nhau tại G. Kết luận nào sau đây là sai?

A. $CG=\frac{2}{3}CN$ ;

B. $GN=\frac{1}{2}GC$ ;

C. $GM=\frac{2}{3}BM$ ;

D. GB=2GM.

Câu 8. Khẳng định nào sau đây là không đúng?

A. Biến cố chắc chắn luôn xảy ra;

B. Biến cố không thể không bao giờ xảy ra;

C. Xác suất của biến cố ngẫu nhiên bằng 1;

D. Biến cố có khả năng xảy ra cao hơn sẽ có xác suất lớn hơn.

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (1,0 điểm) Tìm x, biết:

a) $\frac{3}{x}=\frac{x}{27}$; b) (2x + 3)(x + 2) = (x – 4)(2x + 1)

Bài 2. (2,0 điểm) Cho hai đa thức P(x) = 6x⁵ + 15 – 7x – 4x² – x⁵;

Q(x) = –5x⁵ – 2x + 4x² + 5x – 7.

a) Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.

b) Tìm bậc và hệ số tự do của đa thức K(x) biết K(x) = P(x) – Q(x).

c) Tìm nghiệm của đa thức M(x) biết M(x) = P(x) + Q(x).

Bài 3. (1,0 điểm) Số đo ba góc của một tam giác tỉ lệ với 4; 6; 8. Tính số đo mỗi góc của tam giác đó.

Bài 4. (1,0 điểm) Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:

A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.

B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.

C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.

D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.

a) Trong các biến cố trên, hãy chỉ ra biến cố nào là biến cố chắc chắn, biến cố nào là biến cố không thể.

b) Tính xác suất của biến cố ngẫu nhiên có trong các biến cố A, B, C, D.

Bài 5. (2,5 điểm) Cho ∆ABC cân tại A có $\hat{A}=45°$.

a) Tính số đo các góc của tam giác ABC từ đó so sánh các cạnh của tam giác ABC.

b) Đường trung trực của cạnh AC cắt AB tại D. Trên cạnh AC lấy điểm E sao cho CE = BD. Chứng minh ∆BCD = ∆CBE. Từ đó suy ra $\widehat{BDC}=\widehat{CEB}$.

c) Kẻ đường trung tuyến AM của tam giác ABC. Chứng minh ba đường thẳng AM, BE, CD đồng quy tại một điểm.

Bài 6. (0,5 điểm) Tìm số nguyên x để đa thức A(x) = 2x³ – 3x² + 2x + 2 chia hết cho đa thức B(x) = x² + 1.

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Kết nối tri thức

Năm học 2023

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 4)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Từ đẳng thức $\frac{4}{-5,12}=\frac{2,5}{-3,2}$lập được tỉ lệ thức nào sau đây.

A. $\frac{-3,2}{-5,12}=\frac{2,5}{4}$;

B. $\frac{-5,12}{4}=\frac{2,5}{-3,2}$;

C. $\frac{2,5}{-5,12}=\frac{4}{-3,2}$;

D. $\frac{-5,12}{2,5}=\frac{4}{-3,2}$.

Câu 2. Số hữu tỉ x trong tỉ lệ thức sau: $\frac{2x+3}{24}=\frac{3x-1}{32}$ là

A. x = –15;

B. x = 15;

C. x = –120;

D. x = 120.

Câu 3. Phát biểu nào sau đây sai?

A. Nếu x = –5y thì ta nói x tỉ lệ thuận với y theo hệ số tỉ lệ –5;

B. Nếu $\frac{3}{b}$ thì ta nói b tỉ lệ nghịch với a theo hệ số tỉ lệ 3;

C. Nếu m = n thì ta nói n tỉ lệ thuận với m theo hệ số tỉ lệ 1;

D. Nếu g = 0.h thì ta nói g tỉ lệ nghịch với h theo hệ số tỉ lệ 0.

Câu 4. Biểu thức nào sau đây là biểu thức số?

A. $\frac{1}{x}+y$;

B. xy;

C. x² + y²;

D. 16.(3² + 4).

Câu 5. Cho biểu thức C = –y² + 3x³ + 10. Giá trị của biểu thức C tại x = –1; y = 2 là

A. 9;

B. 11;

C. 3;

D. –3.

Câu 6. Đa thức nào sau đây có bậc là 0?

A. 0;

B. 14;

C. x;

D. 2x – x.

Câu 7. Cho các phát biểu sau:

(I) Biến cố có khả năng xảy ra cao hơn sẽ có xác suất lớn hơn;

(II) Xác suất xảy ra của mỗi kết quả là $\frac{1}{n}$, trong đó n là số các kết quả có khả năng xảy ra bằng nhau của một trò chơi.

Chọn kết luận đúng:

A. Chỉ (I) đúng;

B. Chỉ (II) đúng;

C. Cả (I) và (II) đều đúng;

D. Cả (I) và (II) đều sai.

Câu 8. Cho tam giác ABC có AB = 5 cm, BC = 9 cm và CA = 13 cm. Sắp xếp các góc của ∆ABC theo số đo giảm dần là

A. $\hat{\text{A}};\hat{\text{B}};\hat{\text{C}}$;

B. $\hat{\text{B}};\hat{\text{A}};\hat{\text{C}}$;

C. $\hat{\text{A}};\hat{\text{C}};\hat{\text{B}}$;

D. $\hat{\text{C}};\hat{\text{B}};\hat{A}$.

Câu 9. Bộ ba độ dài nào dưới đây không thể là độ dài ba cạnh của một tam giác?

A. 2 cm, 5 cm, 7 cm;

B. 3 cm, 5 cm, 7 cm;

C. 4 cm, 5 cm, 6 cm;

D. 3 cm, 5 cm, 6 cm.

Câu 10. Trong một tam giác, trực tâm là giao điểm của ba đường gì?

A. Trung trực;

B. Phân giác;

C. Trung tuyến;

D. Đường cao.

Câu 11. Hình lập phương không có đặc điểm nào sau đây?

A. Có 12 cạnh bằng nhau;

B. Có 6 mặt bằng nhau;

C. Có 8 đường chéo;

D. Tất cả các mặt là hình vuông.

Câu 12. Một cái bể dạng hình hộp chữ nhật có chiều dài 1,8 m và chiều rộng bằng $\frac{4}{9}$ chiều dài. Hỏi người ta phải đổ vào trong bể (chưa có nước) đó bao nhiêu lít nước để lượng nước trong bể cao 0,5 m?

A. 720 l;

B. 740 l;

C. 760 l;

D. 780 l.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm) Cho hai đa thức: P(x) = x²(2x³ – 3) + 5x⁴ – 7x³ + x² – x;

Q(x) = 3x⁴ – 2x²(x³ – 3) – 2x³ + x² – 1.

a) Thu gọn và sắp xếp mỗi đa thức trên theo lũy thừa giảm dần của biến.

b) Tìm đa thức R(x) biết P(x) = Q(x) + R(x). Xác định bậc, hệ số cao nhất và hệ số tự do của đa thức R(x).

c) Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không là nghiệm của đa thức Q(x).

Bài 2. (1,0 điểm) Bạn Nam đi mua vở và nhẩm tính với số tiền hiện có thì chỉ mua được 10 quyển vở loại I hoặc 12 quyển vở loại II hoặc 15 quyển vở loại III. Biết rằng tổng giá trị tiền 1 quyển vở loại I và 2 quyển vở loại III nhiều hơn giá tiền 2 quyển vở loại II là 4 000 đồng. Tính giá tiền quyển vở loại III.

Bài 3. (1,0 điểm) Gieo ngẫu nhiên con xúc xắc 6 mặt cân đối một lần. Xét các biến cố:

A: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”;

B: “Số chấm xuất hiện trên con xúc xắc là số chẵn”;

C: “Số chấm xuất hiện trên con xúc xắc chia hết cho 9”.

a) Trong các biến cố trên, biến cố nào là biến cố chắc chắn, biến cố không thể, biến cố ngẫu nhiên?

b) Tính xác suất của biến cố ngẫu nhiên được xác định ở câu a.

Bài 4. (2,5 điểm) Cho ∆ABC cân tại A có hai đường trung tuyến BD và CE cắt nhau tại G.

a) Chứng minh ∆ADB và ∆AEC.

b) Chứng minh ∆GBC là tam giác cân.

c) Chứng minh $GD+GE>\frac{1}{2}BC$.

Bài 5. (0,5 điểm) Tìm giá trị nguyên của x để đa thức 3x³ + 10x² – 5 chia hết cho đa thức 3x + 1.

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Cánh diều

Năm học 2023

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 5)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Bảng sau cho biết số con của 30 gia đình trong khu dân cư:

Điểm không hợp lí trong bảng thống kê trên là

A. Số con trong một gia đình;

B. Số gia đình trong khu dân cư;

C. Tổng số con trong gia đình;

D. Tổng số gia đình được lấy dữ liệu.

Câu 2. Biểu đồ sau cho biết Tổng sản phẩm Quốc nội (GDP) Việt Nam qua các năm:

Biết đóng góp của khu vực kinh tế Công nghiệp và xây dựng vào GDP Việt Nam năm 2019 là 50%. Theo em, khu vực kinh tế này đóng góp bao nhiêu tỉ đô la?

A. 130,5 tỉ đô la;

B. 132,5 tỉ đô la;

C. 134,5 tỉ đô la;

D. 136,5 tỉ đô la.

Câu 3. Gieo hai con xúc xắc và thấy cả hai con xúc xắc đều xuất hiện mặt có số chấm là số chẵn. Trong các biến cố sau, biến cố nào là biến cố chắc chắn?

A. A: “Tổng số chấm trên cả hai con xúc xắc là một số chia 3 dư 1”;

B. B: “Tổng số chấm trên cả hai con xúc xắc là một số chia hết cho 5”;

C. C: “Tổng số chấm trên cả hai con xúc xắc là số chẵn”;

D. D: “Tổng số chấm trên cả hai con xúc xắc là một số lẻ”.

Câu 4. Trong một hộp chứa 15 quả bóng có kích thước và trọng lượng như nhau được đánh số từ 1 đến 15. Lấy ngẫu nhiên 1 quả bóng từ trong hộp. Cho biến cố F: “Lấy được quả bóng đánh số chia hết cho 9”. Xác suất của biến cố F là

A. $P\left(F\right)=\frac{1}{15}$;

B. $P\left(F\right)=\frac{2}{15}$;

C. $P\left(F\right)=\frac{1}{5}$;

D. $P\left(F\right)=\frac{1}{2}$.

Câu 5. Biểu thức x³ + 8 được phát biểu bằng lời là

A. Tổng của x lập phương và 8;

B. Lập phương của tổng x và 8;

C. Ba lần tổng của x và 8;

D. Tổng của ba lần x và 8.

Câu 6. Giá trị của biểu thức: xy(x + y) + (x – y)² tại x = – 4 và y = 2 là

A. 52;

B. 20;

C. – 20;

D. – 52.

Câu 7. Hệ số cao nhất của đa thức N(x) = –x⁴ + 3x + 5 là:

A. –1;

B. 1;

C. 3;

D. 5.

Câu 8. Trong các số sau, số nào là nghiệm của đa thức A(x) = x² – 4?

A. –4;

B. 4;

C. 2;

D. 16.

Câu 9. Cho tam giác ABC có $\hat{A}=60°,\hat{B}=x,\hat{C}=2x.$

Số đo x là bao nhiêu và tam giác ABC là tam giác gì?

A. x = 30° và tam giác ABC là tam giác cân

B. x = 40° và tam giác ABC là tam giác nhọn;

C. x = 80° và tam giác ABC là tam giác tù;

D. x = 90 và tam giác ABC là tam giác vuông.

Câu 10. Cho tam giác ABC có AB < AC. Khẳng định nào dưới đây đúng?

A. $\hat{C}>\hat{B}$;

B. $\hat{C}=\hat{B}$;

C. $\hat{C}<\hat{B}$;

D. $\hat{C}\ge \hat{B}$.

Câu 11. Chọn câu sai?

A. Tam giác vuông có hai cạnh góc vuông bằng nhau được gọi là tam giác vuông cân;

B. Tam giác đều có ba góc bằng nhau và bằng 60°;

C. Hai góc nhọn của tam giác vuông cân bằng nhau và bằng 60°;

D. Một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Câu 12. Nhận xét nào dưới đây sai?

A. Ba đường phân giác của một tam giác cùng đi qua một điểm;

B. Giao điểm ba đường phân giác của một tam giác cách đều ba đỉnh của tam giác đó;

C. Mỗi tam giác có ba đường phân giác;

D. Trong tam giác ABC, tia phân giác của góc A cắt BC tại D. Khi đó AD được gọi là đường phân giác của tam giác ABC.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm) Một đội tình nguyện viên tham gia chống dịch Covid – 19 gồm 40 thành viên đến từ các vùng miền được thống kê trong bảng sau:

a) Lập bảng thống kê tỉ lệ phần trăm số tình nguyện viên tham gia của mỗi vùng miền trong đội tình nguyện viên đó.

b) Vẽ biểu đồ biểu diễn tỉ lệ phần trăm đã tính ở câu a.

c) Chọn ngẫu nhiên một thành viên của đội. Tính xác suất của mỗi biến cố sau:

A: “Thành viên được chọn đến từ vùng Tây Nguyên hoặc Đồng bằng sông Hồng”.

B: “Thành viên được chọn không đến từ vùng Đồng bằng sông Cửu Long”.

Bài 2. (2,0 điểm) Cho đa thức A(x) = – 11x⁵ + 4x³ + 12x² + 11x⁵ – 13x² + 7x + 2.

a) Thu gọn và sắp xếp đa thức A(x) theo số mũ giảm dần của biến.

b) Xác định bậc và hệ số cao nhất của đa thức A(x).

c) Tìm đa thức M(x) sao cho M(x) = A(x) – B(x) biết B(x) = –10 + 2x³ + 3x.

d) Tính M(–1) + M(0).

Bài 3. (3,0 điểm) Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AC, điểm E trên cạnh AC sao cho BD = CE.

a) Chứng minh rằng: AD = AE và $∆$ABE = $∆$ACD.

b) Chứng minh rằng: AI là đường phân giác của góc BAC.

c) Tìm vị trí của hai điểm D và E sao cho BD = DE = EC. Khi đó tìm vị trí của điểm I.

Bài 4. (0,5 điểm) Tìm giá trị nguyên của x để đa thức 4x³ – 4x² – x + 4 chia hết cho đa thức 2x + 1.

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Chân trời sáng tạo

Năm học 2023

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 6)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Chọn câu đúng. Với điều kiện các tỉ số đều có nghĩa thì từ $\frac{x}{y}=\frac{u}{v}$ ta có

A. $\frac{x}{y}=\frac{x+u}{y+v}$;

B. $\frac{x}{y}=\frac{x+u}{y-v}$;

C. $\frac{x}{y}=\frac{x-u}{y+v}$;

D. $\frac{x}{y}=\frac{x-u}{y.v}$.

Câu 2. Giả sử x và y là hai đại lượng tỉ lệ thuận, x₁; x₂ là hai giá trị khác nhau của x và y₁; y₂ là hai giá trị tương ứng của y. Biết y₁ – x₁ = 7 và x₂ = – 4; y₂ = 3, giá trị của x₁; y₁ là

A. x₁ = –28; y₁ = 21;

B. x₁ = –3; y₁ = 4;

C. x₁ = –4; y₁ = 3;

D. x₁ = 4; y₁ = –3.

Câu 3. Cho a, b là các số đã biết không thay đổi giá trị. Các biến trong biểu thức đại số ax + by là

A. a; b;

B. a; b; x; y;

C. x; y;

D. a; x.

Câu 4. Giá trị của biểu thức x + 2x²y – y² tại x = –1 và y = –1 là

A. 0;

B. –4;

C. 2;

D. –2.

Câu 5. Chọn khẳng định đúng.

Xét tam giác ABC có:

A. AB + BC < AC;

B. AC – BC > AB;

C. AB + BC > AC;

D. AB + BC = AC.

Câu 6. Cho tam giác ABC có AH ⊥ BC (H ∈ BC) thì

A. AB > AH;

B. BH = CH;

C. AB < AC;

D. AH < BC.

Câu 7. Cho tam giác ABC với hai đường trung tuyến BM và CN cắt nhau tại G. Kết luận nào sau đây là sai?

A. $CG=\frac{2}{3}CN$ ;

B. $GN=\frac{1}{2}GC$ ;

C. $GM=\frac{2}{3}BM$ ;

D. GB=2GM.

Câu 8. Khẳng định nào sau đây là không đúng?

A. Biến cố chắc chắn luôn xảy ra;

B. Biến cố không thể không bao giờ xảy ra;

C. Xác suất của biến cố ngẫu nhiên bằng 1;

D. Biến cố có khả năng xảy ra cao hơn sẽ có xác suất lớn hơn.

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (1,0 điểm) Tìm x, biết:

a) $\frac{3}{x}=\frac{x}{27}$; b) (2x + 3)(x + 2) = (x – 4)(2x + 1)

Bài 2. (2,0 điểm) Cho hai đa thức P(x) = 6x⁵ + 15 – 7x – 4x² – x⁵;

Q(x) = –5x⁵ – 2x + 4x² + 5x – 7.

a) Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.

b) Tìm bậc và hệ số tự do của đa thức K(x) biết K(x) = P(x) – Q(x).

c) Tìm nghiệm của đa thức M(x) biết M(x) = P(x) + Q(x).

Bài 3. (1,0 điểm) Số đo ba góc của một tam giác tỉ lệ với 4; 6; 8. Tính số đo mỗi góc của tam giác đó.

Bài 4. (1,0 điểm) Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:

A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.

B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.

C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.

D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.

a) Trong các biến cố trên, hãy chỉ ra biến cố nào là biến cố chắc chắn, biến cố nào là biến cố không thể.

b) Tính xác suất của biến cố ngẫu nhiên có trong các biến cố A, B, C, D.

Bài 5. (2,5 điểm) Cho ∆ABC cân tại A có $\hat{A}=45°$.

a) Tính số đo các góc của tam giác ABC từ đó so sánh các cạnh của tam giác ABC.

b) Đường trung trực của cạnh AC cắt AB tại D. Trên cạnh AC lấy điểm E sao cho CE = BD. Chứng minh ∆BCD = ∆CBE. Từ đó suy ra $\widehat{BDC}=\widehat{CEB}$.

c) Kẻ đường trung tuyến AM của tam giác ABC. Chứng minh ba đường thẳng AM, BE, CD đồng quy tại một điểm.

Bài 6. (0,5 điểm) Tìm số nguyên x để đa thức A(x) = 2x³ – 3x² + 2x + 2 chia hết cho đa thức B(x) = x² + 1.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 2

Năm học 2023

Môn: Toán 7

Thời gian làm bài: 90 phút

Bài 1 (2,0 điểm) : Thời gian giải xong một bài tập (tính theo phút) của 30 học sinh được ghi lại trong bảng sau:

a) Lập bảng tần số và tìm mốt của dấu hiệu.

b) Tính số trung bình cộng.

Bài 2 (1,5 điểm) : Cho đơn thức: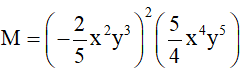

Thu gọn đơn thức M rồi xác định hệ số, phần biến và bậc.

Bài 3 (2,5 điểm) : Cho: P(x) + (3x² - 2x) = x³ + 3x² - 2x + 2020

a) Tính P(x).

b) Cho Q(x) = -x³ + x - 20 . Tính Q(2).

c) Tìm nghiệm của đa thức P(x) + Q(x).

Bài 4 (1,0 điểm) : Nhà Lan cách trường học 650m. Hôm nay Lan giúp mẹ đưa em đi nhà trẻ cách nhà 250m sau đó mới đến trường. Xem hình vẽ và hãy tính khoảng cách từ nhà trẻ đến trường của Lan.

Bài 5 (3,0 điểm) : Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của 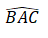(D ∈ BC) . Trên AC lấy điểm E sao cho AE = AB.

a)

Chứng minh rằng: ΔADB = ΔADE rồi suy ra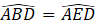

b)

Tia ED cắt AB tại F. chứng minh rằng: AC = AF

c)

Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I.

Chứng minh rằng: DI = 2IH

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 2

Năm học 2023

Môn: Toán 7

Thời gian làm bài: 90 phút

Bài 1 (2,0 điểm) : Điểm kiểm tra 45 phút môn Toán của lớp 7A được cô giáo ghi lại như sau:

a) Dấu hiệu ở đây là gì ?

b) Tính số trung bình cộng và tìm mốt của dấu hiệu.

Bài 2 (1,5 điểm) : Cho đơn thức sau:

a) Thu gọn đơn thức M.

b) Tính giá trị của đơn thức tại x = -1 , y = 3 .

Bài 3 (2,0 điểm) : Cho hai đa thức:

A(x) = x² + 7x⁴ - 2x - 10

B(x) = 3x + 4x⁴ - 2x³ + 7

a) Sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.

b) Hãy tính A(x) + B(x); A(x) - B(x) .

Bài 4 (1,0 điểm) : Trên đường đi học, từ trước nhà đến cổng trường về phía tay phải, Tuấn đếm được tất cả 34 cây cột đèn chiếu sáng. Nếu khoảng cách trung bình 2 cây cột đèn là 35 mét thì quãng đường từ nhà Tuấn đến trường dài bao nhiêu mét ?

Bài 5 (3,5 điểm) : Cho vuông tại A (AB > AC). Trên tia đối của tia AC lấy điểm D sao cho AD = AB, trên tia đối của tia AB lấy điểm E sao cho DE = BC.

a) Chứng minh ΔABC = ΔADE

b) Chứng minh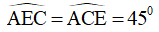

c) Đường cao AH của ΔABC cắt DE tại F. Qua A kẻ đường vuông góc với CF tại G, đường thẳng này cắt đường thẳng BC tại K. Chứng minh: FK // AB.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 2

Năm học 2023

Môn: Toán 7

Thời gian làm bài: 90 phút

PHẦN 1. TRẮC NGHIỆM (2 điểm). Chọn câu trả lời đúng

Câu 1 : Đơn thức -3xy²z(-2x²yz) có bậc là:

A. 3

B. 5

C. 6

D. 8

Câu 2 : Có bao nhiêu câu đúng trong các câu sau

(1) Hai đơn thức -2xy²z và -2xyz² đồng dạng

(2) Đa thức P(x) = -x⁵ + 3x² + x⁵ - x² + 3x⁴ - 5x⁴ có hệ số cao nhất là 3

(3) Đa thức 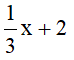có nghiệm là – 6.

Câu 3 : Nếu ΔABC có 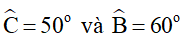thì

A. BC > AB > AC

B. AB > BC > AC

C. BC > AC > AB

D. AC > BC > AB

Câu 4 : Nếu ΔABC có hai đường trung tuyến BM và CN cắt nhau tại I thì

A. Đường thẳng AI vuông góc với BC

B. Tia AI là tia phân giác của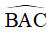

C. IA = IB = IC

D.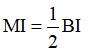

PHẦN II. TỰ LUẬN (8 điểm).

Bài 1 (2,5 điểm) :

Cho các đa thức

P(x) = -x³ + 3x² + x - 1 + 2x³ - x²

Q(x) = -3x³ - x² + 2x³ + 3x + 3 - 4x

a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến

b) Tìm đa thức H(x) = P(x) + Q(x)

c) Tính H(-1) và H(1)

d) Chứng tỏ rằng đa thức H(x) không có nghiệm.

Bài 2 (1,5 điểm) : Cho đa thức f(x) = x² - mx + 3

a) Tìm m để f(x) nhận x = 3 làm một nghiệm

b) Với giá trị vừa tìm đươc của m, hãy tìm nghiệm còn lại của f(x)

Bài 3 (3,5 điểm) : Cho ΔABC vuông tại A, đường phân giác BD. Vẽ DE ⊥ BC (E ∈ BC) .

a) Chứng minh ΔABD = ΔEBD

b) So sánh AD và CD

c) Gọi M là trung điểm AB, N là trung điểm BE. Chứng minh AN, BD, EM đồng quy.

Bài 4 (0,5 điểm) : Cho đa thức f(x) = ax + b (a,b ∈ Z). Chứng minh rằng không thể đồng thời có f(13) = 67 và f(8) = 39

Tải đề thi