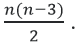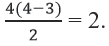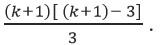Chứng minh số đường chéo của một đa giác lồi n cạnh là n(n-3)/2

Bài 1: Phương pháp quy nạp toán học

Bài 5 trang 83 Toán 11: Chứng minh số đường chéo của một đa giác lồi n cạnh là

Trả lời

Với n = 4, ta có tứ giác.

Thay n = 4 vào công thức, ta có số đường chéo của tứ giác theo công thức là:

Vì tứ giác có hai đường chéo nên công thức là đúng.

Vậy khẳng định là đúng với n = 4.

Giả sử đa giác lồi k cạnh (k ≥ 4) có số đường chéo là: (k(k-3))/2 (giả thiết quy nạp).

Xét đa giác lồi k + 1 cạnh.

Ta phải chứng minh công thức đúng với k + 1, nghĩa là phải chứng minh đa giác lồi k + 1 cạnh có số đường chéo là:

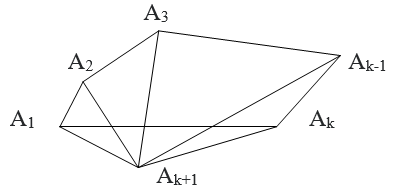
Nối A₁ với A_k ta được đa giác k cạnh A₁A₂…A_k-1 có (k(k-3))/2 đường chéo (giả thiết quy nạp).

Nối A_k+1 với các đỉnh A₂, A₃, …, A_k-1, ta được thêm k – 2 đường chéo, ngoài ra A₁A_k cùng là 1 đường chéo.

Vậy số đường chéo của đa giác k + 1 cạnh là:

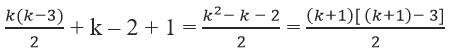
Như vậy, khẳng định cũng đúng với đa giác k + 1 cạnh.

Vây bài toán đã được chứng minh.