Giải Toán 11 trang 82 Kết nối tri thức, Chân trời sáng tạo
Haylamdo giới thiệu lời giải bài tập Toán 11 trang 82 Kết nối tri thức, Chân trời sáng tạo sẽ giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 trang 82.
Giải Toán 11 trang 82 Kết nối tri thức, Chân trời sáng tạo
- Toán lớp 11 trang 82 Tập 1 (sách mới):
- Toán lớp 11 trang 82 Tập 2 (sách mới):
Lưu trữ: Giải Toán 11 trang 82 (sách cũ)
Bài 1 trang 82 Toán 11: Chứng minh rằng n ∈ N* ta có đẳng thức:
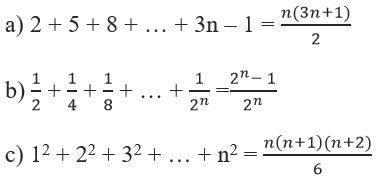
Trả lời
a) Thay n = 1 vào đẳng thức trên ta thấy đẳng thức đúng.
Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là:
2 + 5 + 8 + … + 3k – 1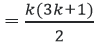 
(1) (giả thiết qui nạp).
Ta phải chứng minh rằng đẳng thức đã cho cũng đúng với n = k + 1, tức là:
2 + 5 + 8 + … + 3k – 1 + 3k + 2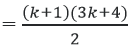 
(2)
Thật vậy từ (1) ta có:
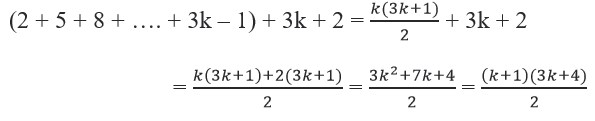
Vậy (2) đúng ⇒ (đpcm)
b) Khi n = 1, đẳng thức đã cho là đúng.
Giả sử đẳng thức đúng với n = k ≥ 1, tức là:
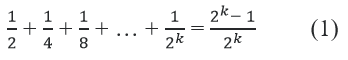
Ta phải chứng minh rằng đẳng thức đã cho cũng đúng với n = k + 1, tức là:
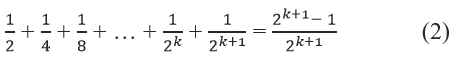
Thật vậy từ (1) ta có:
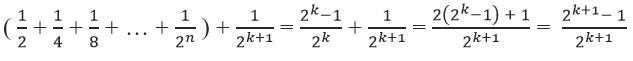
Vậy (2) đúng, từ đó ⇒ (đpcm)
c) Khi n = 1, đẳng thức đã cho là đúng.
Giả sử đẳng thức đúng với n = k ≥ 1, tức là:
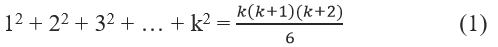
Ta phải chứng minh rằng đẳng thức đã cho cũng đúng với n = k + 1, tức là:
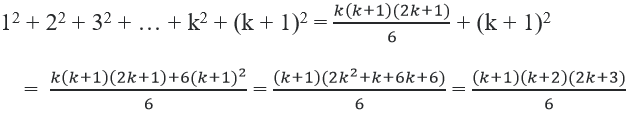
Vậy (2) đúng, từ đó ⇒ (đpcm).
