Bài 12.1, 12.2, 12.3 trang 23 SBT Toán 6 tập 1

Bài 12.1, 12.2, 12.3 trang 23 SBT Toán 6 tập 1

Bài 12.1 trang 23 SBT Toán 6 Tập 1 : Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

a) Nếu a + b + c = 9 thì 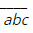⋮ 9;

b) Nếu a + b + c = 18 thì 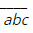⋮ 18;

c) Nếu 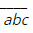⋮ 9 thì a + b + c = 9.

Lời giải:

a) Đúng

b) Sai vì với số 189 có tổng các chữ số bằng 18 nhưng không chia hết cho 18.

c) Sai vì a + b + c có thể bằng 18. Ví dụ số 189

Bài 12.2 trang 23 SBT Toán 6 Tập 1 : Có bao nhiêu số tự nhiên có ba chữ số và chia hết cho 3?

Lời giải:

Số tự nhiên nhỏ nhất có 3 chữ số và chia hết cho 3 là 102.

Số tự nhiên lớn nhất có 3 chữ số và chia hết cho 3 là 999.

Khoảng cách giữa hai số liên tiếp chia hết cho 3 là 3.

Do đó, tổng số các số là: (999 - 102) : 3 + 1 = 300 (số)

Bài 12.3 trang 23 SBT Toán 6 Tập 1 : Cho n = 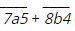. Biết a - b = 6 và n chia hết cho 9. Tìm a và b.

Lời giải:

Ta biết rằng một số và tổng các chữ số của nó có cùng số dư khi chia cho 9.

Tổng 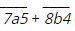chia hết cho 9 nên (7 + a + 5 + 8 + b + 4) ⋮ 9

⇔ 24 + a + b ⋮ 9

=> a + b ∈{3 ; 12}

Vì a - b = 6 nên a + b > 3 do đó a + b = 12 (*).

Từ a - b = 6 suy ra a = 6 + b thay vào (*) ta được:

6 + b + b = 12 => b = 3 => a = 9

Vậy a = 9; b = 3