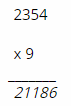Bài 135, 136, 137, 138, 139, 140 trang 23 SBT Toán 6 tập 1

---

Bài 135, 136, 137, 138, 139, 140 trang 23 SBT Toán 6 tập 1

Bài 135 trang 23 SBT Toán 6 Tập 1 : Dùng ba trong bốn chữ số 7, 6, 2, 0 hãy ghép thành các số tự nhiên có ba chữ số sao cho số đó:

a. Chia hết cho 9

b. Chia hết cho 3 mà không chia hết cho 9.

Lời giải:

a. Ta có tổng 3 chữ số:

7 + 6 + 2 = 15 :/. 9

7 + 6 + 0 = 13 :/. 9

7 + 2 + 0 = 9 ⋮ 9

6 + 2 + 0 = 8 :/. 9

Vậy số tự nhiên có ba chữ số chia hết cho 9 là các số được thành lập từ 3 số 7, 2, 0 đó là: 207, 270, 720, 702.

b. Ta có: 7 + 6 + 2 = 15 và 15 ⋮ 3 và 15 :/. 9

Vậy số tự nhiên có ba chữ số chia hết cho 3 mà không chia hết cho 9 là các số được thành lập từ 3 số 2, 7, 6 đó là: 267, 276, 627, 672, 762, 726.

Bài 136 trang 23 SBT Toán 6 Tập 1 : Viết số tự nhiên nhỏ nhất có bốn chữ số sao cho số đó:

Lời giải:

a. Số tự nhiên nhỏ nhất có bốn chữ số chia hết cho 3 có dạng

Ta có: 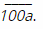⋮ 3 <=> (1 + 0 + 0 + a) ⋮ 3 <=> (1 + a) ⋮ 3

Suy ra: a ∈{2; 5; 8}

Vậy số tự nhiên nhỏ nhất có bốn chữ số chia hết cho 3 là 1002.

b. Số tự nhiên nhỏ nhất có bốn chữ số chia hết cho 9 có dạng

Ta có: 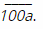⋮ 9 <=> (1 + 0 + 0 + a) ⋮ 9 <=> (1 + a) ⋮ 9

Suy ra: a ∈{8}

Vậy số tự nhiên nhỏ nhất có bốn chữ số chia hết cho 9 là 1008.

Bài 137 trang 23 SBT Toán 6 Tập 1 : Tổng (hiệu) sau có chia hết cho 3, cho 9 không?

a. 10¹² – 1

b. 10¹⁰ + 2

Lời giải:

a. Số 10¹² có tổng các chữ số là 1 + 0 + 0 + … + 0 = 1

* Vì 1 chia cho 3 dư 1 nên 10¹² chia cho 3 dư 1.

=> 10¹² – 1 chia hết cho 3.

* Vì 1 chia 9 dư 1 nên 10¹² chia cho 9 dư 1.

=> 10¹² – 1 chia hết cho 9.

b. Số 10¹⁰ có tổng các chữ số là 1 + 0 + 0 + … + 0 = 1

=> 10¹⁰ + 2 có tổng các chữ số là 1 + 0 + 0 + … + 0 + 2 = 3

Vì 3 chia hết cho 3 nhưng không chia hết cho 9.

Vậy 10¹⁰ + 2 chia hết cho 3 nhưng không chia hết cho 9.

Bài 138 trang 23 SBT Toán 6 Tập 1 : Điền chữ số vào dấu * để được số chia hết cho 3 mà không chia hết cho 9?

a. 53*     b. *471

Lời giải:

a. Ta có: 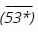⋮ 3 <=> [5 + 3 + (*)] ⋮ 3 <=> [8 + (*)] ⋮ 3

=> (*) ∈ A = {1; 4; 7} (I)

:/. 9 <=> [5 + 3 + (*)] :/. 9 <=> [8 + (*)] :/. 9

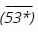
=> (*) ∈B = {0; 2; 3; 4; 5; 6; 7; 8; 9} (II)

Từ (I) và (II) suy ra: (*) ∈A ∩ B = {4; 7}

Vậy ta được các số: 534; 537.

b. Ta có 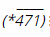⋮ 3 <=> [(*) + 4 + 7 + 1] ⋮ 3 <=> [12 + (*)] ⋮ 3

=> (*) ∈C = {0; 3; 6; 9} (III)

Vì (*) ở chữ số hàng nghìn nên (*) khác 0. Suy ra: (*) = {3; 6; 9}

:/. 9 <=> [(*) + 4 + 7 + 1] :/. 9 <=> [12 + (*)] :/. 9

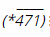
=> (*) ∈D = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} (IV)

Từ (III) và (IV) suy ra: (*) ∈C ∩ D = {3; 9}

Vậy ta được các số: 3471; 9471.

Bài 139 trang 23 SBT Toán 6 Tập 1 : Tìm chữ số a và b sao cho a – b = 4 và 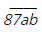⋮ 9

Lời giải:

Ta có: 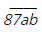⋮ 9 <=> (8 + 7 + a + b) ⁝ 9 <=> (15 + a + b) ⁝ 9

Suy ra: (a + b) ∈{3; 12}

Vì a – b = 4 nên a + b > 3. Suy ra a + b = 12

Thay a = 4 + b vào a + b = 12, ta có:

b + (4 + b) = 12 <=> 2b = 12 – 4

<=> 2b = 8 <=> b = 4

a = 4 + b = 4 + 4 = 8

Vậy ta có số: 8784.

Bài 140 trang 23 SBT Toán 6 Tập 1 : Điền vào dấu * các chữ số thích hợp:

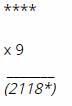
Lời giải:

Vì **** x 9 = 2118* nên (2118*) ⋮ 9

<=> [2 + 1 + 1 + 8 + (*)] ⋮ 9 <=> [12 + (*)] ⋮ 9

Vì (*) là số tự nhiên có một chữ số nên (*) = 6.

Vậy 21186 : 9 = 2354