Bài 1.1, 1.2, 1.3, 1.4 trang 37 SBT Toán 7 tập 2

Bài 1.1, 1.2, 1.3, 1.4 trang 37 SBT Toán 7 tập 2

Bài 1.1: Tam giác ABC có ∠A là góc tù, ∠B > ∠C. Trong các khẳng định sau, khẳng định nào đúng?

(A) AB > AC > BC

(B) AC > AB > BC

(C) BC > AB > AC

(D) BC > AC > AB

Lời giải:

Do ∠A là góc tù nên ∠A lớn nhất. Vậy có ∠A > ∠B > ∠C. Từ đó suy ra BC > AC > AB. Chọn (D) BC > AC > AB.

Bài 1.2: Tam giác ABC có AB = 5cm, BC = 6cm và AC = 7cm. Gọi ∠A , ∠B , ∠C theo thứ tự là góc ngoài tại đỉnh A, B, C của tam giác đó. Trong các khẳng định sau, khẳng định nào đúng?

(A) ∠A > ∠B > ∠C

(B) ∠B > ∠C > ∠A

(C) ∠C > ∠A > ∠B

(D) ∠C > ∠B > ∠A

Lời giải:

Chọn C

Bài 1.3: So sánh các cạnh của một tam giác cân, biết rằng nó có một góc ngoài bằng 40°.

Lời giải:

Theo giả thiết, tam giác cân này có một góc ngoài bằng 40° nên nó có một góc trong bằng 180° - 40° = 140°. Góc trong này không thể là góc ở đáy của tam giác cân mà phải là góc ở đỉnh. Vậy cạnh đáy của tam giác cân lớn hơn hai cạnh bên của nó.

Bài 1.4: Cho tam giác ABC với AB ≥ AC. Trên cạnh BC lấy một điểm M bất kỳ khác B và C. Chứng minh rằng AM < AC.

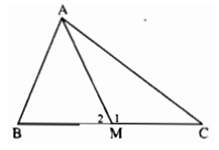
Lời giải:

Ta có ∠M₁ + ∠M₂ = 180° nên chỉ có hai khả năng xảy ra ứng với các vị trí của M trên BC là ∠M₁ > 90° hoặc ∠M₂ ≥ 90°.

- Nếu ∠M₁ > 90° thì tam giác AMC có góc tù nên AM > AC

- Nếu ∠M₂ ≥ 90° thì trong tam giác ABM có AM < AB. Kết hợp với giả thiết AB < AC, ta suy ra AM < AC. Vậy ta luôn có AM < AC.