Bài 6, 7, 8, 9, 10 trang 37 SBT Toán 7 tập 2

Bài 6, 7, 8, 9, 10 trang 37 SBT Toán 7 tập 2

Bài 6: Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh các độ dài AD, DC.

Lời giải:

Kẻ DH ⊥ AC.

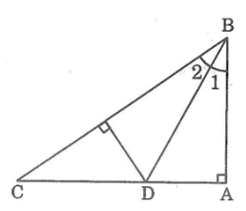
Xét hai tam giác vuông ABD và HBD, ta có:

∠B₁ = ∠B₂ (gt)

Cạnh huyền BD chung

Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)

⇒ AD = HD (2 cạnh tương ứng)    (1)

Trong tam giác vuông DHC có ∠DHC = 90°

⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền)    (2)

Từ (1) và (2) suy ra: AD < DC

Bài 7: Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. So sánh ∠(BAM) và ∠(MAC)

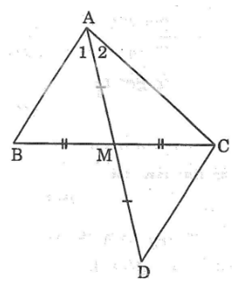
Lời giải:

Trên tia đối tia MA lấy điểm D sao cho MD = MA

Xét ΔAMB và ΔDMC, ta có:

MA = MD (theo cách vẽ)

∠(AMB) = ∠(DMC) (đối đỉnh)

MB = MC (gt)

Suy ra: ΔAMB = ΔDMC (c.g.c)

Suy ra: AM = CD (2 cạnh tương ứng)

và ∠D = ∠A₁ (2 góc tương ứng)    (1)

Mà AB < AC (gt)

nên: CD < AC

Trong ΔADC, ta có: CD < AC

Suy ra: ∠D > ∠A₂ (đối diện cạnh lớn hơn là góc lớn hơn)    (2)

Từ (1) và (2) suy ra: ∠A₁ > ∠A₂ hay ∠(BAM) > ∠(MAC) .

Bài 8: Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở D. So sánh các độ dài BD, DC.

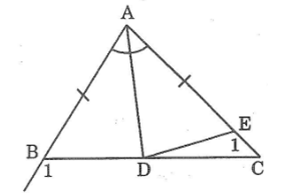
Lời giải:

Trên cạnh AC lấy điểm E sao cho AE = AB.

Ta có: AB < AC nên AE < AC

Suy ra E nằm giữa A và C.

Xét ΔABD và ΔAED, ta có:

AB = AE (theo cách vẽ)

∠(BAD) = ∠(EAD) (gt)

AD cạnh chung

Suy ra: ΔABD = ΔAED (c.g.c)

Suy ra: BD = DE (2 cạnh tương ứng)

và ∠(ABD) = ∠(AED) (2 góc tương ứng)

Mà: ∠(ABD) + ∠B₁ = 180° (2 góc kề bù)

∠(AED) + ∠E₁ = 180° (2 góc kề bù)

Suy ra: ∠B₁ = ∠E₁

Trong ΔABC ta có ∠B₁ là góc ngoài tại đỉnh B

Ta có: ∠B₁ > ∠C (tính chất góc ngoài của tam giác)

Suy ra: ∠E₁ > ∠C

Suy ra: DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)

Vậy BD < DC.

Bài 9: Chứng minh rằng nếu một tam giác vuông có một góc nhọn bằng 30° thì cạnh góc vuông đối diện với nó bằng nửa cạnh huyền.

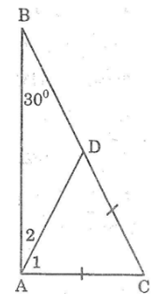
Lời giải:

Xét ΔABC, ta có: ∠A = 90°; ∠B = 30°

Trên cạnh BC lấy điểm D sao cho CD = AC

Ta có: ΔACD cân tại C

Mà ∠C + ∠B = 90° (tính chất tam giác vuông)

Suy ra: ∠C = 90° - ∠B = 90° - 30° = 60°

Suy ra: ΔACD đều

Suy ra: AC = AD = DC và ∠A₁ = 60°

Ta có: ∠A₁ + ∠A₂ = ∠BAC = 90°

⇒ ∠A₂ = 90° - ∠A₁ = 90° - 60° = 30°

Trong ΔADB, ta có: ∠A₂ = ∠B = 30°

Suy ra: ΔADB cân tại D (vì có 2 góc kề cạnh AB bằng nhau)

Hay AD = DB

Suy ra: AC = CD = DB mà CD + DB = BC

Vậy AC = 1/2 BC.

Bài 10: Chứng minh định lý “Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn” theo gợi ý sau:

Cho tam giác ABC có ∠B > ∠C

a. Có thể xảy ra AC < AB hay không?

b. Có thể xảy ra AC = AB hay không?

Lời giải:

a. Nếu AB > AC thì ∠C > ∠B (góc đối diện với cạnh lớn hơn là góc lớn hơn)

Điều này trái với giả thiết ∠B > ∠C nên không xảy ra.

b. Nếu AB = AC thì ΔABC cân tại A

⇒ ∠B = ∠C(tính chất tam giác cân)

Điều này trái với giả thiết ∠B = ∠C nên không xảy ra.

Vậy ∠B > ∠C hay AC > AB.