Bài 31, 32, 33, 34, 35 trang 42 SBT Toán 7 tập 2

Bài 31, 32, 33, 34, 35 trang 42 SBT Toán 7 tập 2

Bài 31: Cho hình dưới. Điền vào chỗ trống:

GK = … CK; AG = … GM; GK = … CG; AM = … AG; AM = … GM

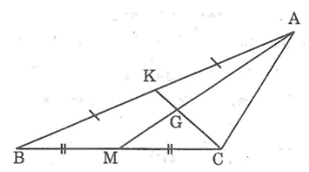
Lời giải:

GK = 1/3 CK; AG = 2GM; GK = 1/2 CG; AM = 3/2 AG; AM = 3GM

Bài 32: Chứng minh rằng nếu một tam giác có hai trung tuyến bằng nhau thì tam giác đó là tam giác cân.

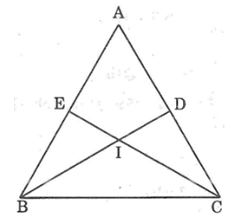
Lời giải:

Giả sử ΔABC có hai đường trung tuyến BD và CE bằng nhau.

Gọi I là giao điểm BD và CE, ta có:

BI = 2/3 BD (tính chất đường trung tuyến)    (1)

CI = 2/3 CE (tính chất đường trung tuyến)    (2)

Từ (1), (2) và giả thiết BD = CE suy ra: BI = CI

Suy ra: BI + ID = CI + IE ⇒ ID = IE

Xét ΔBIE và ΔCID, ta có:

BI = CI (chứng minh trên)

∠(BIE) = ∠(CID) (đối đỉnh)

IE = ID (chứng minh trên)

Suy ra: ΔBIE = ΔCID (c.g.c)

Suy ra: BE = CD (hai cạnh tương ứng)    (3)

Lại có: BE = 1/2 AB (vì E là trung điểm AB)    (4)

CD = 1/2 AC (vì D trung điểm AB)    (5)

Từ (3), (4) và (5) suy ra: AB = CD.

Vậy tam giác ABC cân tại A.

Bài 33: Tam giác ABC cân tại A có AB = CD = 34cm, BC = 32cm. Kẻ đường trung tuyến AM.

a. Chứng minh rằng AM ⊥ BC.

b. Tính độ dài AM

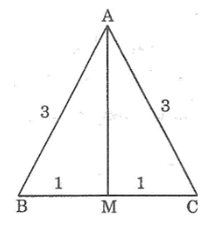
Lời giải:

a. Xét ΔAMB và ΔAMC, ta có:

AM = AC (gt)

BM = CM (gt)

AM cạnh chung

Suy ra: ΔAMB = ΔAMC (c.c.c)

Suy ra: ∠(AMB) = ∠(AMC)    (1)

Lại có: ∠(AMB) + ∠(AMC) = 180° (hai góc kề bù)    (2)

Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90°

Vậy AM ⊥ BC.

b. Tam giác AMB có ∠(AMB) = 90°

Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:

AB² = AM² + BM² ⇒ AM² = AB² - BM² = 34² - 16²

= 1156 - 256 = 900

Suy ra: AM = 30 (cm).

Bài 34: Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng:

a. Các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.

b. Các đường trung tuyến của tam giá BGD bằng một nửa các cạnh của tam giác ABC.

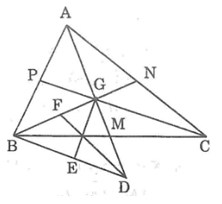
Lời giải:

a. Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.

Ta có: AG = GD (gt)

AG = 2GM (tính chất đường trung tuyến)

Suy ra: GD = 2GM

Mà GD = GM + MD ⇒ GM = MD

Xét ΔBMD và ΔCMG, ta có:

BM = CM (gt)

∠(BMD) = ∠(CMG) (đối đỉnh)

MD = GM (chứng minh trên)

Suy ra: ΔBMD = ΔCMG (c.g.c)

⇒ BD = CG (hai cạnh tương ứng)

Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)

Suy ra: BD = 2/3 CP    (1)

Lại có: BG = 2/3 BN (tính chất đường trung tuyến)    (2)

Và AG = 2/3 AM (tính chất đường trung tuyến)

Suy ra: GD = 2/3 AM    (3)

Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.

b. Ta có: GM = MD (chứng minh trên)

Suy ra BM là đường trung tuyến của tam giác BGD.

Suy ra: BM = 1/2 BC    (4)

Kẻ đường trung tuyến GE và DF của tam giác BGD, ta có:

FG = 1/2 BG (tính chất đường trung tuyến)

GN = 1/2 GB (tính chất đường trung tuyến)

Suy ra: FG = GN

Xét ΔDFG và ΔANG, ta có:

AG = GD (gt)

∠(DGF) = ∠(AGN) (đối đỉnh)

GF = GN (chứng minh trên)

Suy ra: ΔDFG = ΔANG (c.g.c) ⇒ DF = AN

Mà AN = 1/2 AC (gt)

Suy ra: DF = 1/2 AC    (5)

Mặt khác: BD = CG (chứng minh trên)

ED = 1/2 BD (vì E là trung điểm BD)

GP = 1/2 CG (tính chất đường trung tuyến)

Suy ra: ED = GP

Lại có: ΔBMD = ΔCMG (chứng minh trên)

⇒ ∠(BDM) = ∠(CGM) hay ∠(EDG) = ∠(CGM)

(CGM) = (PGA) (đối đỉnh)

Suy ra: ∠(EDG) = ∠(PGA)

AG = GD (gt)

Suy ra: ΔPGA = ΔEDG (c.g.c) ⇒ GE = AP mà AP = 1/2 AB (gt)

Do đó: GE = 1/2 AB    (6)

Từ (4), (5) và (6) suy ra các đường trung tuyến của ΔBGD bằng một nửa cạnh của ΔABC.

Bài 35: Tam giác ABC có BC = 10cm, các đường trung tuyến BD và CE. Chứng minh rằng BD + CE > 15cm.

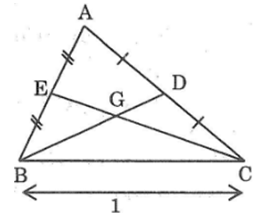
Lời giải:

Gọi G là giao điểm của BD và CE.

Trong ΔGBC, ta có:

GB + GC > BC (bất đẳng thức tam giác)

GB = 2/3 BD (tính chất đường trung tuyến)

GC = 2/3 CE (tính chất đường trung tuyến)

Mà BC = 10 cm (gt)

Suy ra: 23 (BD + CE) > 10 hay BD + CE > 10 : 2/3 = 10.3/2 = 15

Vậy BD + CE > 15 (cm).