Bài 2.5, 2.6 trang 40 SBT Toán 7 tập 2
Bài 2.5, 2.6 trang 40 SBT Toán 7 tập 2
Bài 2.5: Cho điểm A nằm ngoài đường thẳng xy
a) Tìm trên đường thẳng xy hai điểm M, N sao cho hai đường xiên AM và AN bằng nhau.
b) Lấy một điểm D trên đường thẳng xy. Chứng minh rằng:
- Nếu D ở giữa M và N thì AD < AM ;
- Nếu D không thuộc đoạn thẳng MN thì AD > AM.
Lời giải:
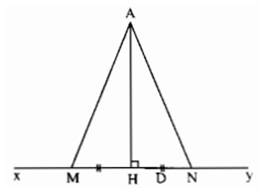
a) Phân tích bài toán: Giả sử M và N là hai điểm của đường thẳng xy mà AM = AN. Nếu gọi H là chân đường vuông góc kẻ từ điểm A đến xy thì HM, HN lần lượt là hình chiếu của các đường xiên AM, AN.
Từ AM = AN suy ra HM = HN, từ đó xác định được hai điểm M, N.
Kẻ AH vuông góc với xy (H ∈ xy)
Lấy hai điểm M, N trên xy sao cho HM = HN (1)
(dùng compa vẽ một đường tròn tâm H bán kính tùy ý; đường tròn này cắt đường thẳng xy tại hai điểm M, N thỏa mãn HM = HN)
Hai đường xiên AM, AN lần lượt có hình chiếu là HM và HN, do đó từ (1) suy ra AM = AN
b) Xét trường hợp D ở giữa M và N
- Nếu D ≡ H thì AD = AH, suy ra AD > AM (đường vuông góc ngắn hơn đường xiên)
- Nếu D ở giữa M và H thì HD < HM, do đó AD < AM (đường xiên có hình chiếu ngắn hơn thì ngắn hơn)
- Nếu D ở giữa H và N thì HD < HN, do đó AD < AN.
Theo a) ta có AM = AN nên AD < AM
Vậy khi D ở giữa M và N thì ta luôn có AD < AM
Bài 2.6: Cho điểm P nằm ngoài đường thẳng d.
a) Hãy nêu cách vẽ đường xiên PQ, PR sao cho PQ = PR và ∠(QPR) = 60°
b) Trong hình dựng được ở câu a), cho PQ = 18cm. Tính độ dài hình chiếu của hai đường xiên PQ, PR trên d.
Lời giải:

a) Phân tích bài toán
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và ∠(QPR) = 60°. Gọi H là chân đường vuông góc kẻ từ P đến d. Khi đó ΔPHQ = ΔPHQ (cạnh huyền, cạnh góc vuông), suy ra ∠(HPQ) = ∠(HPR) = 30°. Từ đó suy ra cách vẽ hai đường xiên PQ và PR.
Kẻ PH ⊥ d (H ∈ d). Dùng thước đo góc để vẽ góc HPx bằng 30°. Tia Px cắt d tại điểm Q. Trên d lấy điểm R sao cho HR = HQ. Hai đường xiên PQ và PR lần lượt có hình chiếu trên d là HQ và HR. Do HQ = HR nên PQ = PR.
Hơn nữa ∠(QPR) = 2∠(HPQ) = 60°.
b) Hướng dẫn
- Tam giác PQR có PQ = PR và ∠(QPR) = 60°, tam giác đó là tam giác gì?
- PQ = 18cm ⇒ QR =? ; HQ = HR =?

