Viết phương trình tiếp tuyến của parabol: trang 205 sgk Đại Số và Giải Tích 11 nâng cao

Luyện tập trang 204-205

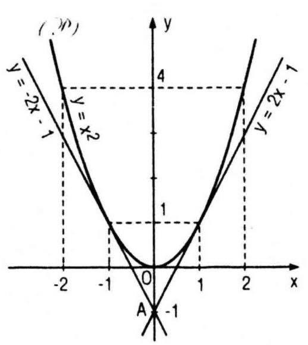
Bài 25 (trang 205 sgk Đại Số và Giải Tích 11 nâng cao): (P) Viết phương trình tiếp tuyến của parabol y = x², biết rằng tiếp tuyến đó đi qua A(0 ;-1)

Hướng dẫn : Trước hết viết phương trình tiếp tuyến tại điểm có hoành độ x_o thuộc parabol đã cho. Sau đó tìm x_o để tiếp tuyến đi qua A(chú ý rằng điểm A không thuộc parabol)

Lời giải:

Đặt f(x) = x² và gọi M_o là điểm thuộc (P)với hoành độ x_o . Khi đó tọa độ điểm M_o là (x_o ; f(x_o)) hay (x_o ; x_o²)

Cách 1 : Ta có y’=2x . phương trình tiếp tuyến của (P)tại điểm M_o là : y = 2x_o(x – x_o) + x_o² ⇔ y = 2x_ox – x_o²

Tiếp tuyến đó đi qua A(0 ;-1) nên ta có : - 1 = 2x_o.0 – x_o²

⇔ -1 = -x₀² ⇔ x₀² = 1 ⇔ x₀ = ±1

+Với x_o = 1 thì f(x_o) = 1, f’(x_o) = 2 và phương trình tiếp tuyến cần tìm là :

y = 2(x – 1) + 1 ⇔ y = 2x – 1

+Với x_o = -1 thì f(x_o) = 1, f’(x_o) = -2 và phương trình tiếp tuyến cần tìm là :

y = -2(x + 1) + 1 ⇔ y = -2x – 1

Vậy có hai tiếp tuyến của (P) đi qua A với các phương trình tương ứng là y = ±2x – 1

Cách 2 :Phương trình đường thẳng (d) đi qua A(0 ;-1) với hệ số góc k là :

y = k(x - 0) + (-1) hay y = kx - 1

Để (d) tiếp xúc (P)tại điểm M(x₀; y₀) điều kiện cần và đủ là (xem bài tập 13)

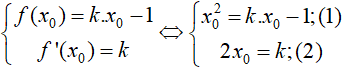
Thay (2) vào (1) ta được:

x_o² = 2x_ox_o - 1 ⇔ x_o² = 1 ⇔ x_o = ± 1

+) Với x_o = 1 thì k = 2.

Khi đó, phương trình tiếp tuyến cần tìm là:

y= 2x – 1

+) Với x_o = -1 thì k = -2.

Khi đó, phương trình tiếp tuyến cần tìm là:

y = - 2x – 1 .