Giải các phương trình sau: trang 42 sgk Đại Số và Giải Tích 11 nâng cao

Bài 3: Một số dạng phương trình lượng giác đơn giản

Bài 36 (trang 42 sgk Đại Số và Giải Tích 11 nâng cao): Giải các phương trình sau:

a) tan(x/2) = tanx

b) tan(2x + 10^o) + cotx = 0

c) (1 - tanx)(1 + sin2x) = 1 + tanx

d) tanx + tan2x = sin3xcosx

e) tanx + cot2x = 2cot4x

Lời giải:

a)

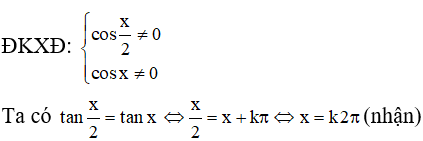
b)

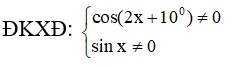
tan(2x + 10^o) + cotx = 0 ⇔ tan(2x + 10^o) = tan(90^o + x)

⇔ 2x + 10^o = 90^o + x + k.180^o ⇔ x = 80^o + k.180^o

Hiển nhiên x = 80^o + k.180^o thỏa mãn ĐKXĐ.

Vậy phương trình đã cho có nghiệm x = 80^o + k.180^o

c)

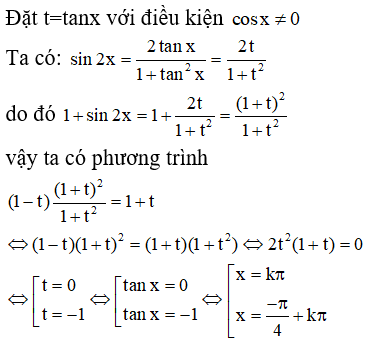
d) v

e) ĐKXĐ: cosx ≠ 0, sin2x ≠ 0, sin4x ≠ 0 nhưng chỉ cần sin4x ≠ 0 là đủ vì sin4x = 2sin2xcos2x = 4sinxcosxcos2x. Với điều kiện đó ta có:

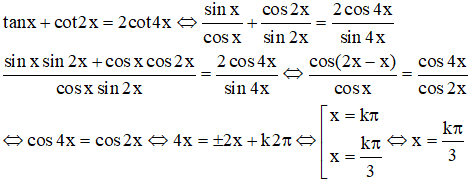
Để là nghiệm các giá trị này còn phải thỏa mãn sin4x ≠ 0 . Ta có:

- Nếu k chia hết cho 3 tức là k = 3m, thì sin4x = sin4mπ = 0

- Nếu k không chia hết cho 3, tức là k = 3m + 1 , m ∈ Z thì :