Chứng minh rằng: trang 190 sgk Giải Tích 12 nâng cao

Bài 1: Số phức

Haylamdo biên soạn và sưu tầm lời giải Bài 8 trang 190 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 8 (trang 190 sgk Giải Tích 12 nâng cao): Chứng minh rằng:

a) Nếu vectơ u→ của một mặt phẳng phức biểu diễn số phức z thì độ dài của vectơ u→ là |u→ |=|z|, từ đó nếu các điểm A₁;A₂ theo thức tự biểu diễn các số phức z₁;z₂ thì |A₁A₂→ |=|z₂-z₁ |

b) Với mọi số phức z, z’ ta có |zz' |=|z||z' | và khi z ≠ 0 thì

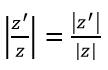
c) Với mọi số phức z, z’ ta có |z+z' |≤|z|+|z' |

Lời giải:

a) Nếu u→ là vectơ biểu diễn số phức z = a + bi thì u→=(a;b)

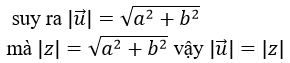
Gọi A₁ là điểm biểu diễn số phức Z₁=a₁+b₁ i=>A₁ (a₁;b₁)

A₂ là điểm biểu diễn số phức Z₂=a₂+b₂ i=>A₂ (a₂;b₂)

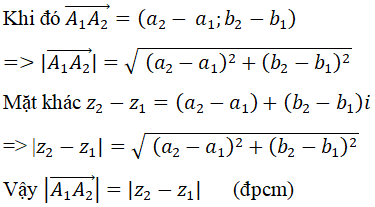
b) Ta có: z.z’=(a+bi)(a'+b' i)=(aa'-bb' )+(ab'+a' b)i

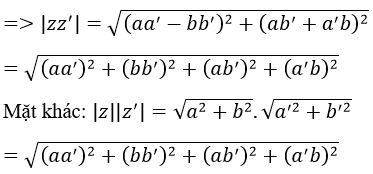
Vậy |zz' |=|z||z' |

* Khi z≠0 nên |z| > 0 theo trên ta có: |zz^' |=|z||z^' |

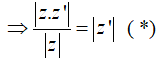
Đặt 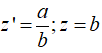(trong đó a, b là hai số thực và b ≠ 0)

Khi đó ( *) trở thành: 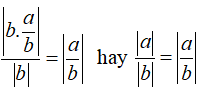( đpcm)

c) Với mọi số phức z, z’, ta có: z + z’ = (a +a’) + (b +b’)i

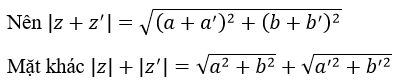
Theo yêu cầu bài toán ta cần chứng minh:

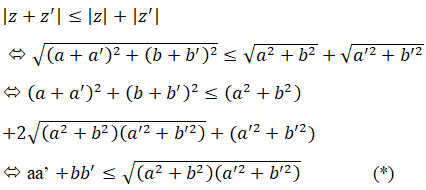
Theo Bu-nhi-cốp-xki ta có bất đẳng thức (*) đúng với ∀a,b,a',b'∈R nên |z+z'| ≤ |z|+|z'| (đpcm)